Первообразная и неопределенный интеграл

Интегральное исчисление

Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Разнообразные вопросы математического анализа, его многочисленные приложения в геометрии, механике, физике и технике приводят к решению обратной задачи: по данной функции 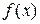найти такую функцию 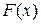, производная которой была бы равна функции 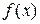, т. е.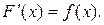

Определение. Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех x из этого промежутка

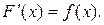
Определение. Если функция F(x) – первообразная для функции f(x), то множество функций F(x)+C, где С – произвольная постоянная, называется неопределенным интегралом от функции f(x) и обозначается символом

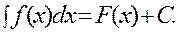
При этом функция f(x) называется подынтегральной функцией, 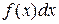– подынтегральным выражением, а переменная х – переменной интегрирования.

Восстановление функции по ее производной или отыскание неопределенного интеграла по данной подынтегральной функции называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.

Дата добавления: 2015-06-26