Устойчивость и синергетика модели Самуэльсона—Хикса

.

.

Устойчивость линейного динамического звена

Устойчивость линейных динамических систем

Система называется устойчивой, если ее реакция на импульсное воз­действие затухает, т.е. импульсная характеристика g(t) имеет нулевую асимптоту:

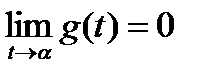(1.3.16)

В конце § 1.2 была найдена импульсная характеристика инерционного звена 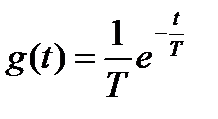, которая затухает в бесконечности, поэтому инерционное звено устойчиво. Исходя из этого устойчива и экономика, описываемая динамической моделью Кейнса, посколь­ку эта модель в непрерывном времени — инерционное звено.

Импульсная характеристика звена является решением следующего уравнения:

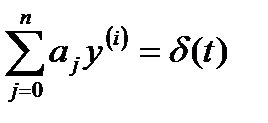. (1.3.17)

Найдем преобразование Лапласа от обеих частей уравнения (1.3.17):

Образ импульсной характеристики

Характеристический многочлен 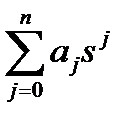имеет п корней 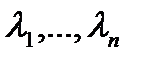(обозначения соответствуют характеристическому уравнению

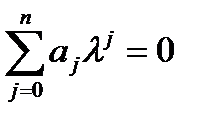) и может быть разложен на следующие множители:

.

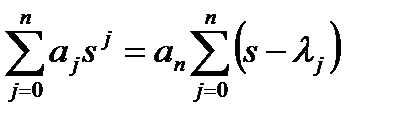Если среди корней встречаются комплексные, то они взаимно сопряженные, например, 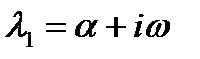, 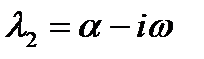. В таком случае множители с парой таких корней можно представить в виде квад­ратного трехчлена:

.

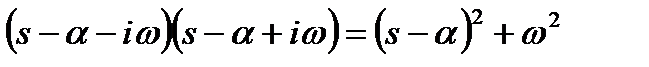Исходя из этого, образ импульсной характеристики линейного звена примет вид (сначала располагаем комплексные корни, затем —

действительные):

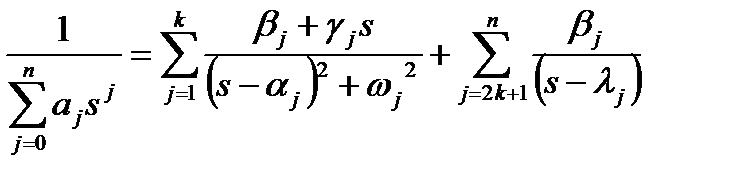, (1.3.18)

где k — число пар взаимно сопряженных корней;

(n - 2 k) — число действительных корней;

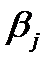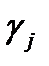, — коэффициенты разложения (1.3.18), которые определяются

путем приведения правой части (1.3.18) к общему

знаменателю, равному .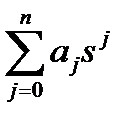

Из разложения (1.3.18) вытекает следующий вид импульсной характеристики динамического звена как прообраза (1.3.18) (снова воспользуемся табл. 1.1):

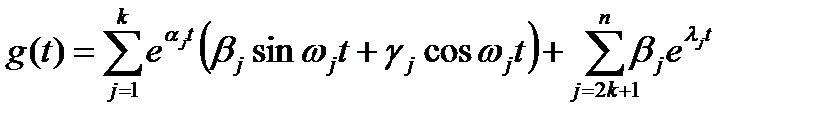. (1.3.19)

Из (1.3.19) видно, что динамическое звено устойчиво, т.е.

,

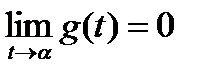если отрицательны действительные части комплексных корней 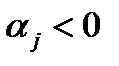, 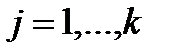и действительные корни 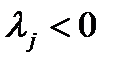, j= 2k+1,.., n.

Ниже в качестве примера детально исследуем условия устойчи­вости модели Самуэльсона—Хикса. Кроме того, покажем, что эта модель при определенных значениях параметров является синергетической, хотя и является линейной динамической системой второ­го порядка.

В работе [1] синергетические свойства экономики трактуются следующим образом: «…синергетическая экономика придает особое значение не линейным, а нелинейным аспектам экономического эволюционного процесса, не устойчивости, а неустойчивостям, не непрерывности, а разрывам, не постоянству, а структурным изме­нениям — в противоположность традиционному рассмотрению ли­нейности, устойчивости, непрерывности и неизменности». К важ­нейшим аспектам экономического эволюционного процесса автор относит «...нелинейность, неустойчивость, бифуркации и хаос в ди­намических экономических системах».

Выше (см. (1.2.18)) было показано, что непрерывным аналогом модели Самуэльсона—Хикса является следующее линейное неодно­родное уравнение второго порядка:

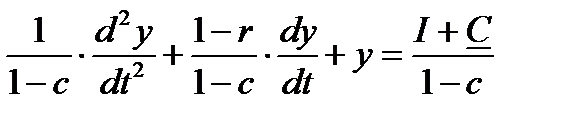(1.3.20)

Согласно теории линейных дифференциальных уравнений [2] общее решение неоднородного уравнения есть сумма общего реше­ния однородного и частного решения неоднородного.

Общее решение однородного уравнения есть линейная комби­нация фундаментальных решений ,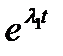

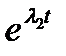
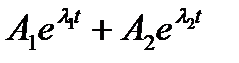, (1.3.21)

где 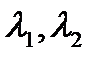— корни характеристического уравнения

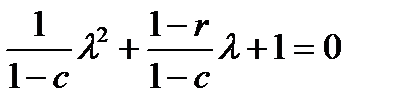. (1.3.22)

которое получается при поиске решения однородного уравнения в виде .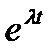

Поскольку частным решением неоднородного уравнения служит константа в правой части (1.3.20), то общее решение неоднородно­го уравнения имеет вид:

.

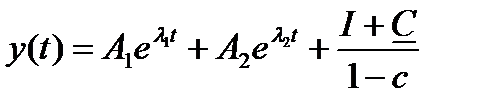Конкретное решение получаем при заданных начальных ус­ловиях.

Выбранное частное решение неоднородного уравнения является одновременно и его стационарным решением

,

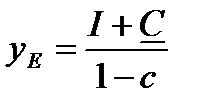а точка 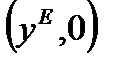на плоскости 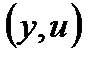переменной у и ее производной

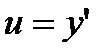является точкой равновесия.

Исследуем поведение решения уравнения (1.3.20) в окрестности точки равновесия 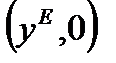. Казалось бы, что при небольшом откло­нении от этой точки, вызванном некоторым внешним импульсным воздействием 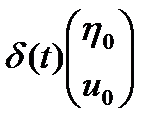, система, попавшая в точку 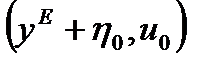, должна после завершения переходного процесса снова возвратиться в точку равновесия 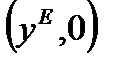. Однако, как будет показано ниже, это далеко не всегда так.

Далее для определенности будем рассматривать случай 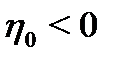, , 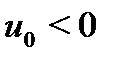как это показано на рис. 1.18, т.е. значение ВВП уменьши­лось, а скорость его роста с нулевой в устойчивом состоянии поме­нялась на отрицательную.

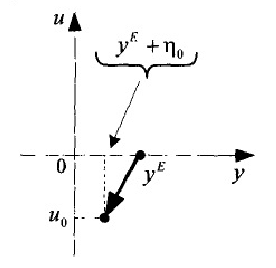
Рис. 1.18. Перевод системы да установившегося состояния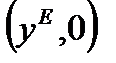

в неустойчивое состояние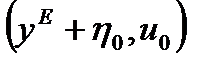

Представим решение уравнения (1.3.20) при начальных условиях

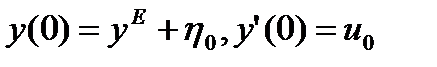в следующем виде:

,

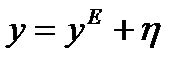тогда приращение ВВП относительно стационарного решения 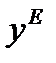будет удовлетворять однородному уравнению

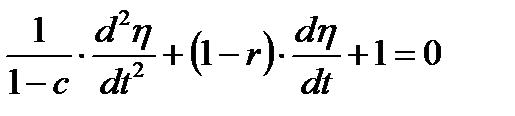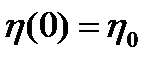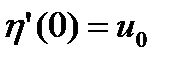, , (1.3.23)

Ниже кроме поведения ВВП будет также изучаться эволюция ин­вестиций и потребления. Согласно модели годовые инвестиции со­стоят из постоянной части I и переменной части 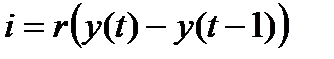. За время 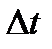переменная часть составит

.

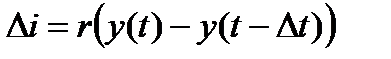Перейдя к пределу при 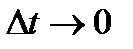, получаем

.

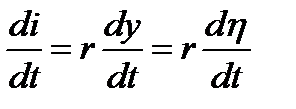Поскольку i (0) = 0, η (0) = 0, то

.

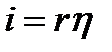Тем самым текущее значение инвестиций

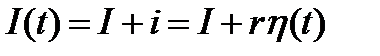, (1.3.24)

а текущее значение потребления как разность ВВП и инвестиций равно соответственно

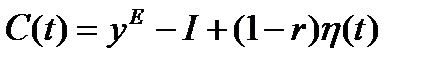. (1.3.25)

Решение однородного уравнения (1.3.23) при заданных началь­ных условиях имеет вид (1.3.21), где 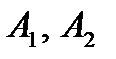определяются из начальных условий. Характер решения зависит от типа корней харак­теристического уравнения (1.3.21), а тип последних в свою очередь обусловливается значением параметров 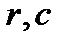. Вначале рассмотрим все возможные значения r при условии, что

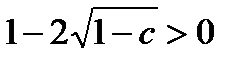, или 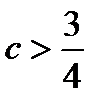. (1.3.26)

Следует заметить, что исследование устойчивости уравнения (1.3.20) было схематически выполнено в [3]. В настоящей работе это исследование проводится в деталях, чтобы выявить случаи синергетического поведения системы.

П е р в ы й с л у ч а й: .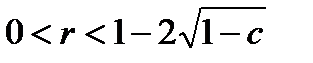

В этом случае дискриминант характеристического уравнения положителен, а его корни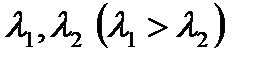

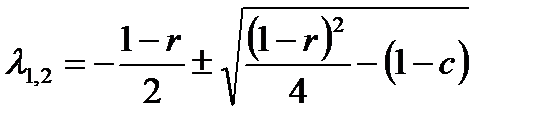, (1.3.27)

действительны и отрицательны, поскольку больший корень 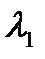при

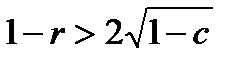отрицателен.

Используя начальные условия (1.3.23), находим

,

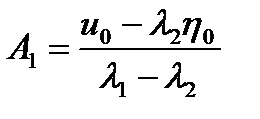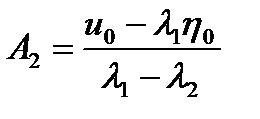
Поэтому

.

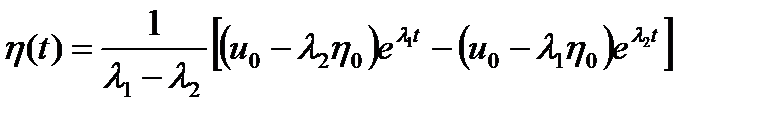Поскольку , , то

.

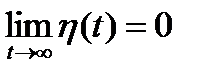Отсюда

,

.

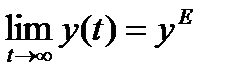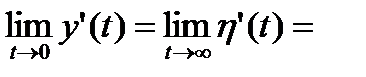
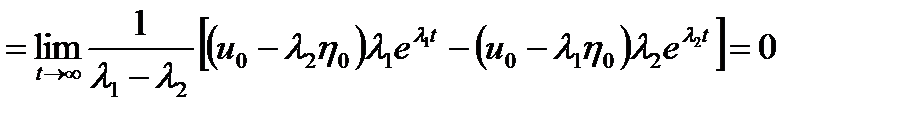Таким образом, система по завершении апериодического пере­ходного процесса возвращается в прежнее состояние покоя ,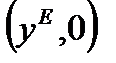

т.е. является устойчивой.

В начале переходного процесса при 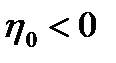, 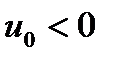ВВП, а следовательно, потребление и инвестиции, продолжают еще некоторое время убывать, затем начинается их монотонный рост, который заканчивается достижением их стационарных значений 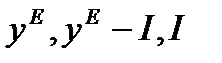соответственно.

В т о р о й с л у ч а й: .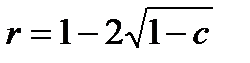

В этом случае дискриминант равен нулю, и характеристическое

уравнение имеет один корень 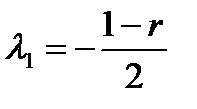кратности два, поэтому фундаментальными решениями однородного уравнения (1.3.20) являются , .

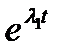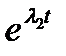Следовательно, общее решение имеет вид:

.

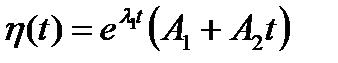Используя начальные условия (1.3.23), находим

, ,

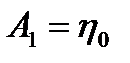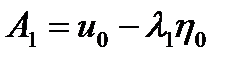поэтому

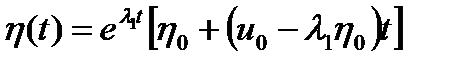
Поскольку 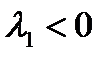, то

,

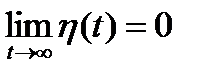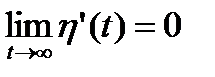
Отсюда

, ,

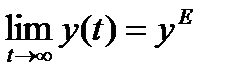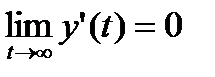т.е. система возвращается в прежнее состояние покоя и, следователь­но, является устойчивой.

ВВП, потребление и инвестиции ведут себя на протяжении пе­реходного процесса аналогично их поведению в первом случае.

Т р е т и й с л у ч а й: .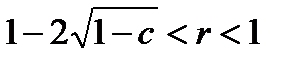

В этом случае дискриминант характеристического уравнения от­рицателен, поэтому его корни комплексные взаимно сопряженные:

, ,

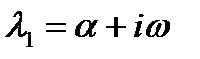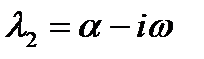где , ,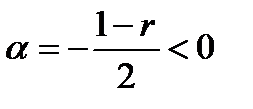

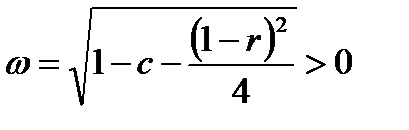Используя начальные условия (1.3.23), находим

, ,

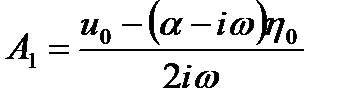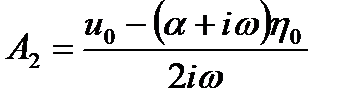поэтому

.

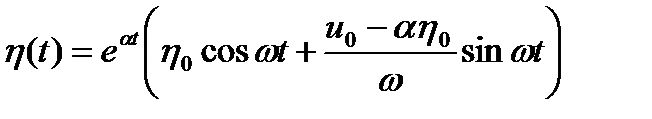Поскольку 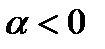, то

,

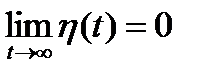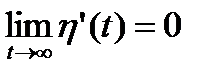
Отсюда

, ,

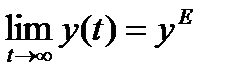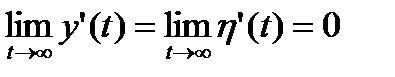Таким образом, система после затухающих гармонических коле­баний возвращается в первоначальное состояние покоя, т.е. является устойчивой.

ВВП, потребление, инвестиции при 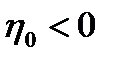, 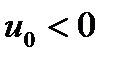вначале продолжают убывать, затем растут и достигают установившихся значе­ний, после чего этот автоколебательный процесс продолжается с экспоненциально затухающей амплитудой вплоть до окончательного достижения этими показателями за бесконечный промежуток вре­мени своих стационарных значений.

Ч е т в е р т ы й с л у ч а й: r =1.

С содержательной точки зрения этот случай означает, что весь прирост ВВП за год целиком идет на инвестиции.

При r =1 корни характеристического уравнения мнимые вза­имно сопряженные:

, , .

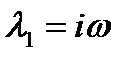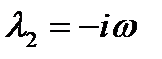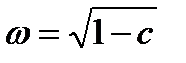Используя начальные условия, находим

, ,

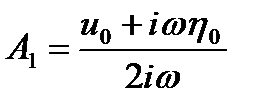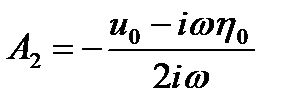поэтому

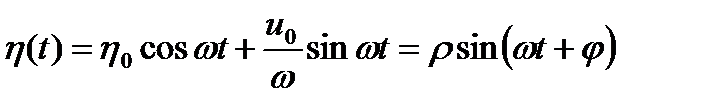, (1.3.28)

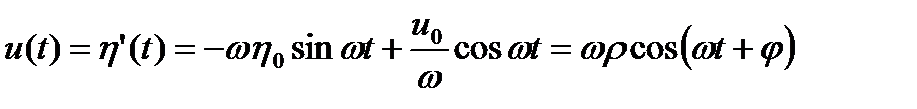, (1.3.29)

где

,

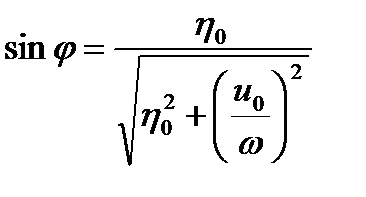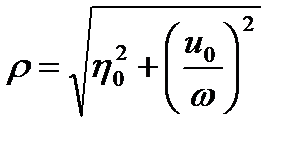
Таким образом, при r =1система будет находиться в незату­хающих гармонических колебаниях, т.е. система неустойчива, по­скольку не возвращается в первоначальное устойчивое состояние, а потому является синергетической.

На плоскости фазовых переменных траектория системы, заданная уравнениями (1.3.28), (1.3.29), будет выглядеть как эллипс в канонической форме (рис. 1.19):

,

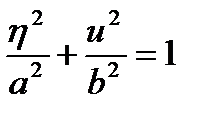где .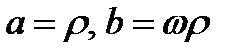

ВВП будет колебаться в пределах 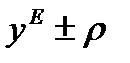, потребление — оставаться постоянным и равным стационарному значению 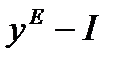, а инвестиции — находиться в незатухающих автоколебаниях со­гласно уравнению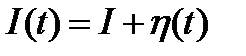

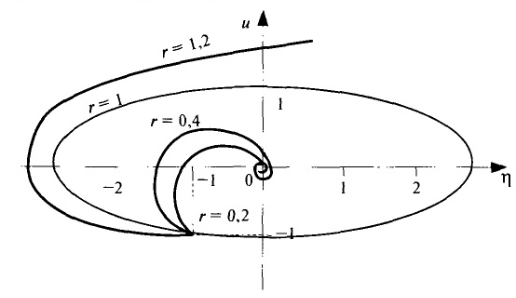
Рис. 1.19. Фазовые траектории системы при разных значениях коэффициента акселерации r (с = 0,84, , )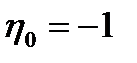

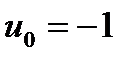П я т ы й с л у ч а й: .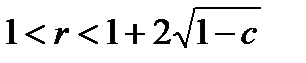

Это запредельный случай, поскольку на дополнительные инве­стиции (сверх постоянного значения I) пойдет больше, чем прирост ВВП, и это превышение может осуществиться лишь за счет соот­ветствующего сокращения потребления.

В этом случае дискриминант характеристического уравнения от­рицателен, поэтому его корни комплексные взаимно сопряженные:

, ,

, .

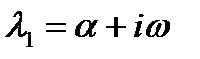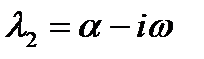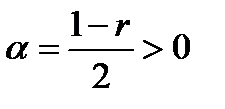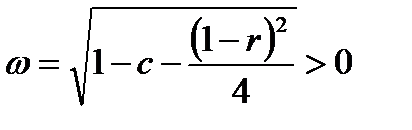Следовательно,

, , ,

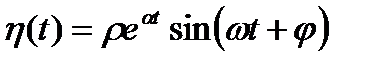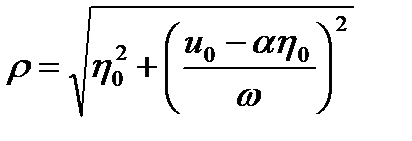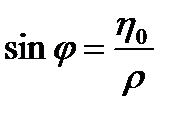т.е. система будет находиться в гармонических автоколебаниях с экспоненциально возрастающей амплитудой, иными словами, сис­тема неустойчивая, синергетическая.

Потребление и инвестиции также будут находиться в гармони­ческих автоколебаниях с экспоненциально возрастающей амплиту­дой вокруг своих стационарных значений:

,

.

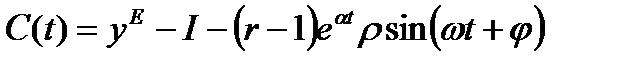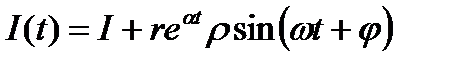На рис. 1.19 для всех рассмотренных случаев показаны траекто­рии системы на плоскости фазовых переменных , .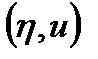

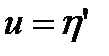Таким образом, экономика, описываемая моделью Самуэльсона—Хикса, устойчива при 0< r <1 и обладает синергетическим свойством (неустойчива) при .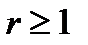

Дата добавления: 2015-06-04