Учет сбережений населения в упрощенной модели Кейнса

Выше нами была рассмотрена процедура линеаризации нели­нейной односвязной системы. Рассмотрим теперь линеаризацию нелинейной двухсвязной системы.

Для описания модели, как и ранее, введем следующие обозна­чения:

у — валовой внутренний продукт (ВВП);

r — процентная ставка на деньги (норма прибыли на деньги);

I_D(y,r), M(y,r) — функции спроса на инвестиции и деньги;

S(y,r) — функция сбережений населения;

М_S — предложение денег (фиксированная величина).

Спрос на инвестиции растет с ростом ВВП, т.е. 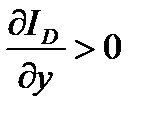, но падает с ростом процентной ставки 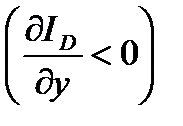. Напротив, сбережения населения растут и при росте ВВП, и при росте процентной ставки, т.е. , .

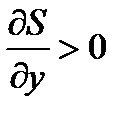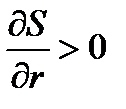Спрос на деньги растет с ростом ВВП (денег должно быть столько, чтобы их с учетом оборота хватило для покупки произведенного ВВП), но падает с ростом нормы процента, т.е. , .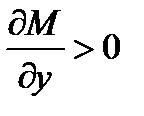

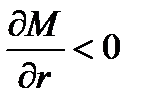Тогда модель делового цикла Кейнса можно записать в следую­щем виде:

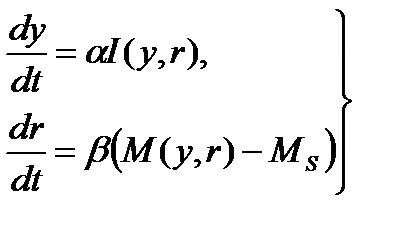, (1.5.9)

где 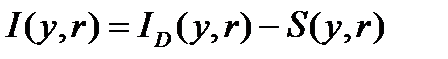— реальные инвестиции, ;

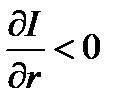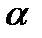— коэффициент реакции ВВП на увеличение реальных

инвестиций ;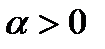

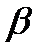— коэффициент реакции процентной ставки на дефицит

денег, .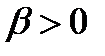

Система (1.5.9) имеет естественную точку равновесия, опреде­ляемую как решение системы двух нелинейных алгебраических уравнений с двумя неизвестными:

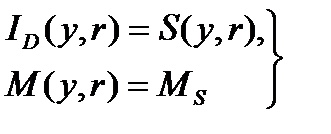, (1.5.10)

Обозначим через 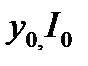решение системы (L5.10) и исследуем поведение динамической системы (1.5.9) в окрестности точки рав­новесия .

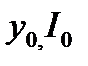Введем новые переменные 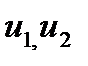как приращения старых отно­сительно координат точки равновесия:

, .

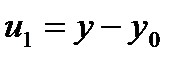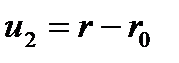Тогда в окрестности нулевой точки система (1.5.9) запишется в следующем виде:

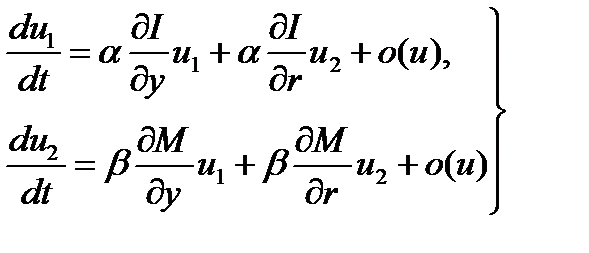, (1.5.11)

где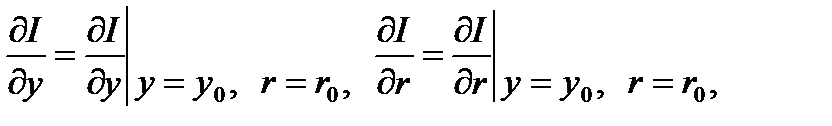

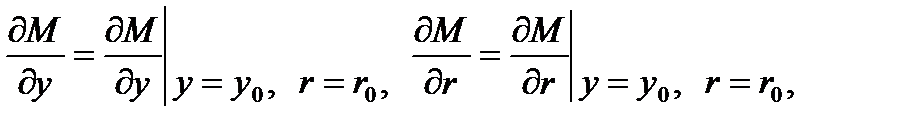
где 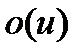— члены более высокого порядка малости, чем .

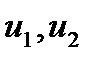Система (1.5.11) — это линейная двухсвязная система с точно­стью до членов 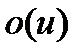. Как описано в § 1.4, будем искать ее решение

в виде

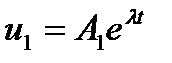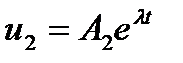, . (1.5.12)

После подстановки выражений (1.5.12) в систему (1.5.11) полу­чим с точностью до :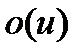

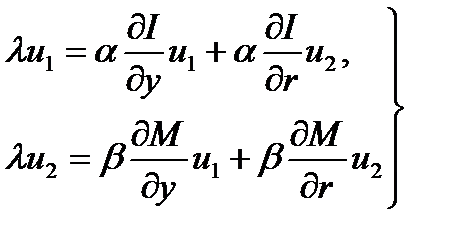. (1.5.13)

Для того чтобы линейная система двух однородных алгебраиче­ских уравнений относительно 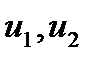имела ненулевое решение, не­обходимо, чтобы ее определитель был равен нулю:

.

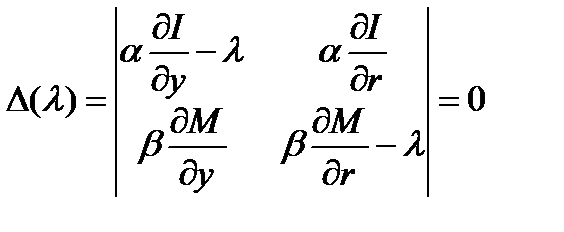Таким образом, получим характеристическое уравнение линеа­ризованной двухсвязной системы:

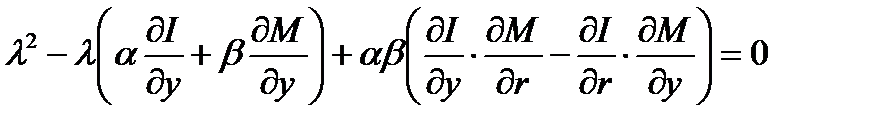(1.5.14)

которое имеет следующее решение:

,

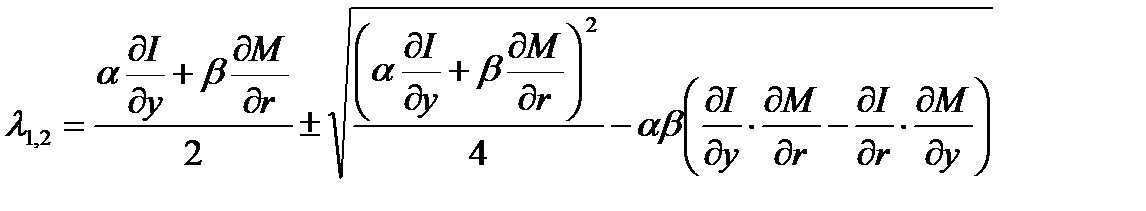Чисто математическую сторону исследования в соответствии с § 1.4 выполним при следующих типовых обозначениях:

, ,

, ,

, .

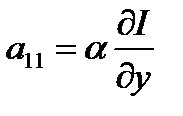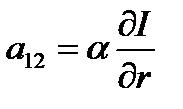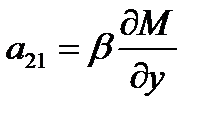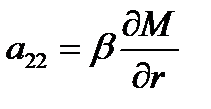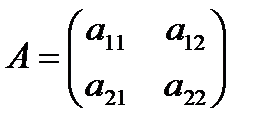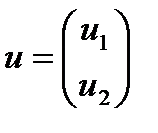Тогда с учетом введенных типовых обозначений и при отбрасы­вании членов 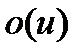система из двух линейных однородных диффе­ренциальных уравнений (1.5.11) запишется следующим образом;

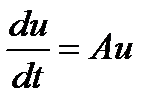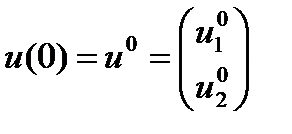, , (1.5.15)

где 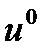— состояние системы в начальный момент времени.

Применив преобразование Лапласа с параметром s к обеим час­тям уравнения (1.5.15), получим

,

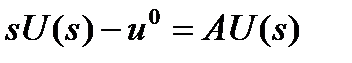где .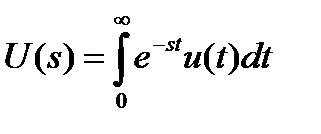

Отсюда

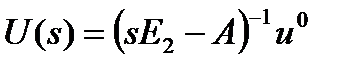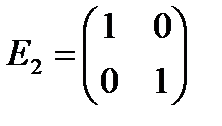, . (1.5.16)

Находим по правилу обращения матрицы

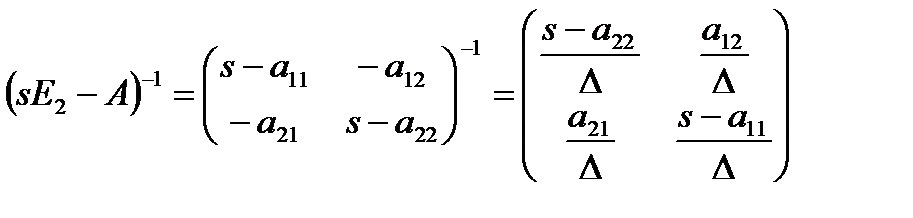, (1.5.17)

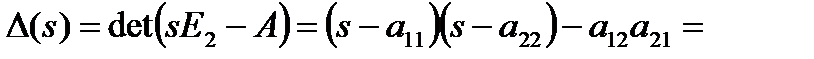
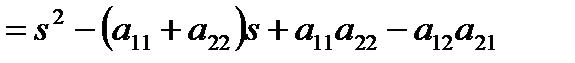. (1.5.18)

Подставив выражение для обратной матрицы в (1.5.16), получаем

,

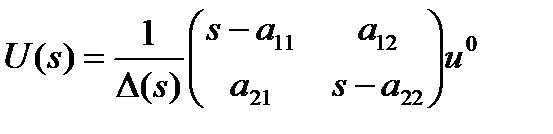откуда

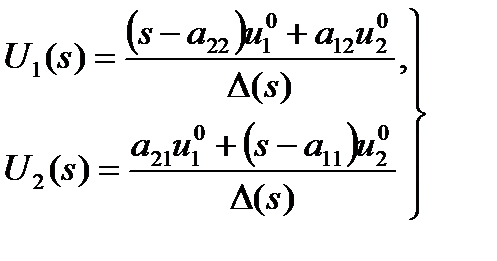. (1.5.19)

Выражения (1.5.19) — это образ решения системы (1.5.15) при

начальных условиях 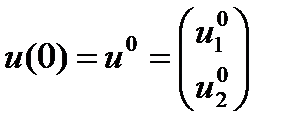. Само решение — это реакция линейной двухсвязной системы (1.5.15) на импульсное воздействие 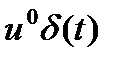в начальный момент времени ( 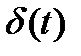— дельта-функция). Если система устойчива, то после завершения переходного процесса она должна возвратиться в первоначальное нулевое 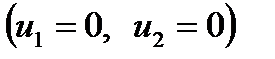стояние покоя. Если же система неустойчива, то она не вернется в первоначальное нулевое состояние.

Поведение системы, как: это видно из полученного образа ре­шения (1.5.19), зависит от корней характеристического многочлена, поскольку , , .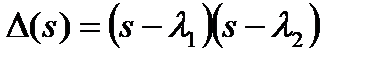

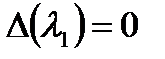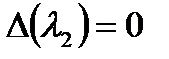Далее рассмотрим три возможных случая:

1) корни мнимые: , , ;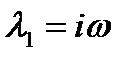

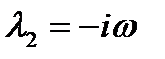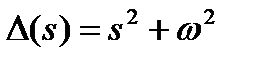2) корни комплексные: , , ;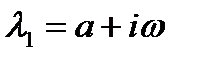

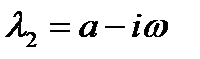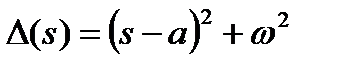3) корни действительные: , .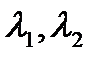

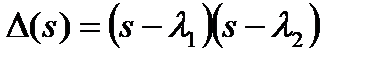Корни мнимые. Деловой цикл Кейиса. Если

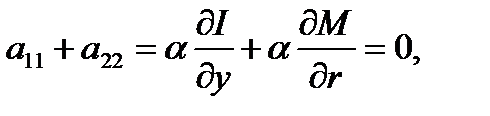(1.5.20)

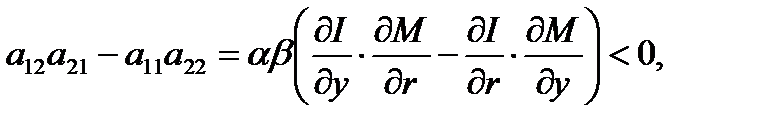(1.5.21)

то

, ,

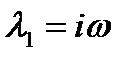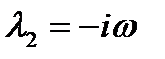где .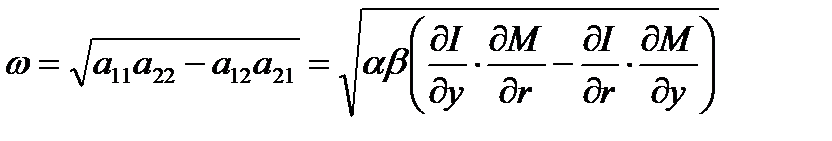

Поэтому в этом случае .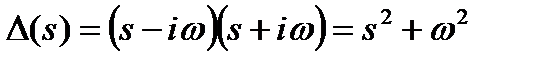

Поскольку согласно табл. 1.1 прообразом 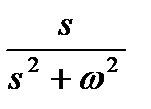является 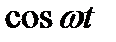, а прообразом 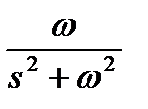— 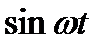, то окончательно получаем:

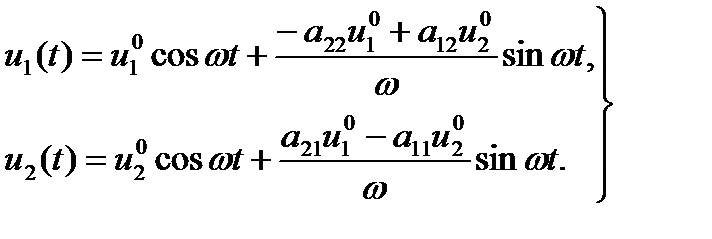(1.5.22)

Таким образом, система будет описывать замкнутый цикл, на­чиная с точки 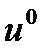, проходя через точку 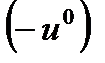и возвращаясь через 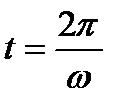снова в точку 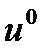. Этот замкнутый цикл показан на рис. 1.20.

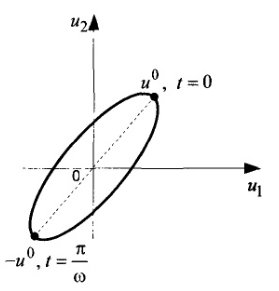
Рис. 1.20. Деловой цикл Keйнca

Вернемся к экономической интерпретации условий возникно­вения делового цикла Кейнса. Прежде всего рассмотрим условие (1.5.20), записав его в виде

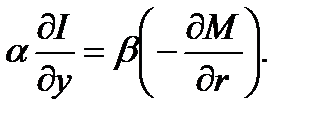
Поскольку 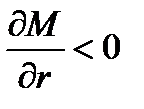, то из этого условия вытекает, что 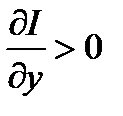,т.е. скорость роста (по ВВП) спроса на инвестиции должна быть больше соответствующей скорости сбережений, кроме того, должно выполняться равенство

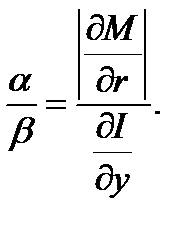
Условие отрицательности дискриминанта

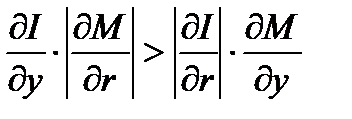
выполняется, по крайней мере, тогда, когда

,

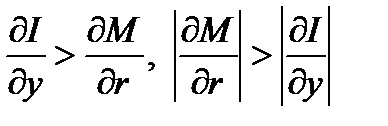т.е. скорость роста (по ВВП) реальных инвестиций выше скорости роста спроса на деньги, а скорость падения (по норме процента) спроса на деньги выше скорости падения реальных инвестиций.

Корни комплексные. Если дискриминант характеристического уравнения (1.5.14) отрицателен, то корни уравнения комплексные взаимно сопряженные:

,

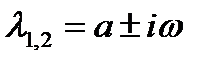где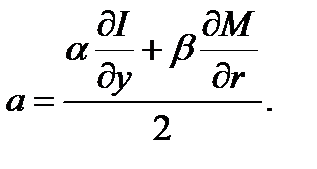

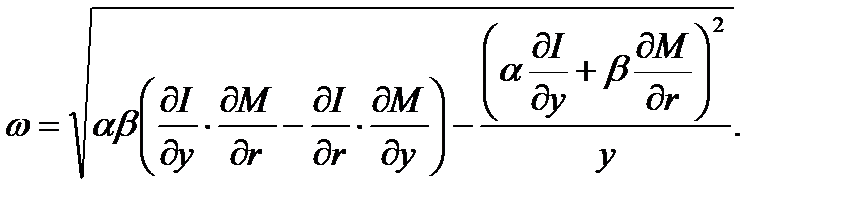
При этом

.

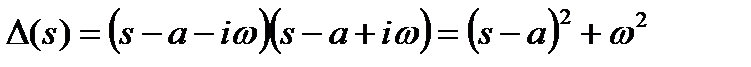В этом случае поведение системы зависит от знака действительной части корней:

• если знак положителен, то имеют место автоколебания с экспоненциально возрастающей амплитудой, и система удаляется от точки равновесия;

• если знак отрицателен, то имеют место автоколебания с экспоненциально убывающей амплитудой, и система возвращается в точку равновесия.

Докажем это. Образ решения будет иметь вид:

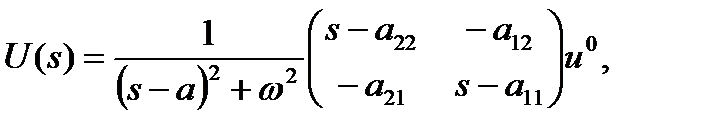
поэтому образы переменных 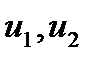соответственно равны

, .

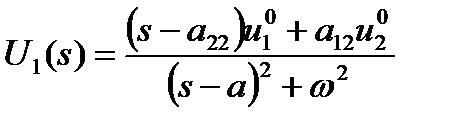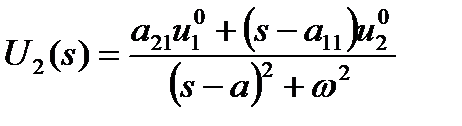Поскольку согласно табл. 1.1 прообразом 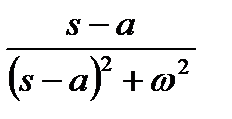является 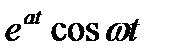, а прообразом 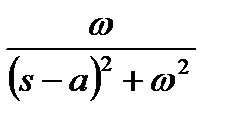— 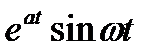, то окончательно получаем

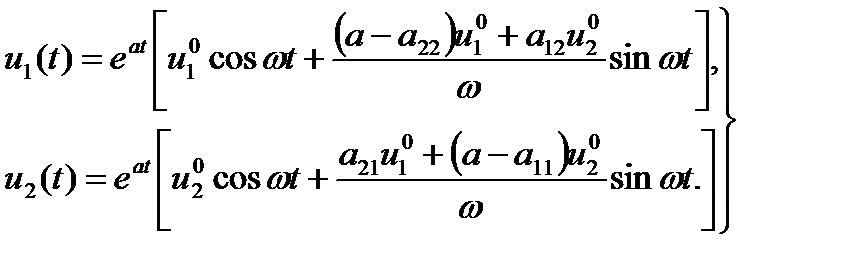(1.5.23)

Члены в квадратных скобках задают автоколебания, а множи­тель e^at определяет экспоненциальное изменение амплитуды: при а > 0 — ее неограниченное увеличение, при а < 0 — ее уменьшение до нуля. Поведение системы в том и другом случаях показано на рис. 1.21 (пунктиром показан разделительный цикл).

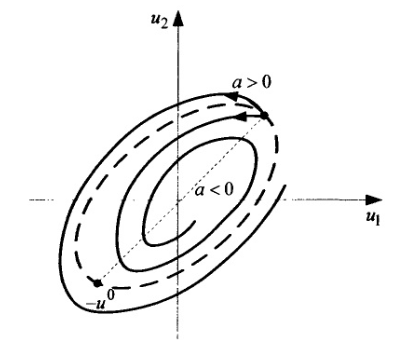
Рис. 1.21. Фазовые траектории системы при комплексных корнях характеристического уравнения

Вернемся к содержательной интерпретации условий возникно­вения рассматриваемой ситуации. Основное условие — отрицатель­ность дискриминанта, что эквивалентно неравенству

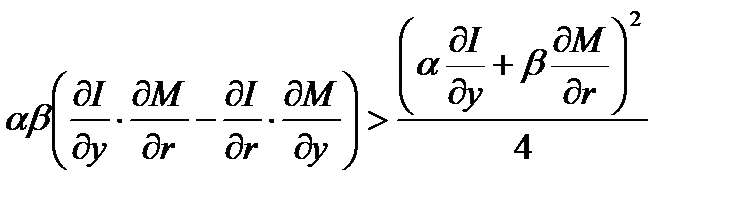. (1.5.24)

Необходимым условием выполнения (1.5.24) является положи­тельность левой части данного неравенства:

,

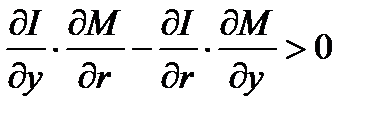или

,

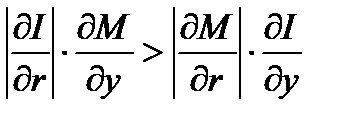Последнее неравенство выполняется, по крайней мере, в том случае, когда

,

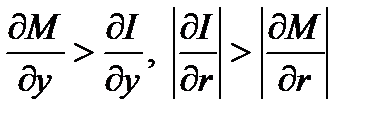т.е. спрос на деньги растет (по у) быстрее, чем реальные инвестиции, а реальные инвестиции падают (по r) быстрее, чем спрос на деньги.

Если дискриминант отрицателен, то поведение системы цели­ком определяется знаком действительности части корней

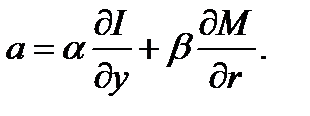
При 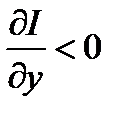, т.е. когда спрос на инвестиции растет (по у) быстрее сбережений населения, то а <0, поскольку .

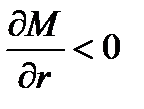Действительная часть корней останется отрицательной, если

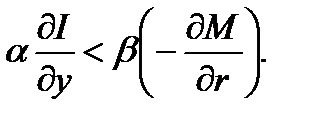
В этом случае система в результате затухающих колебаний вер­нется в первоначальное состояние равновесия .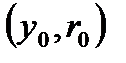

Корни действительные. Если дискриминант характеристическо­го уравнения положителен, то оба корня действительны, поэтому 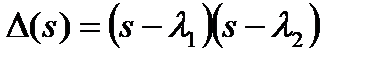, 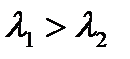и 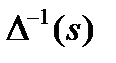можно разложить на простые дроби:

.

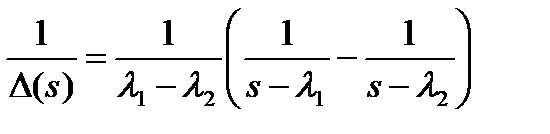Образ решения примет вид:

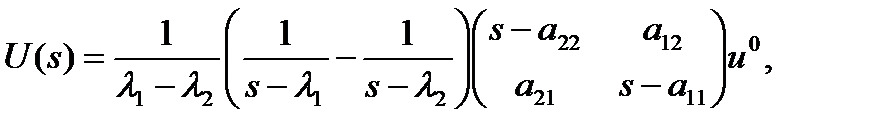
Отдельные его компоненты

, .

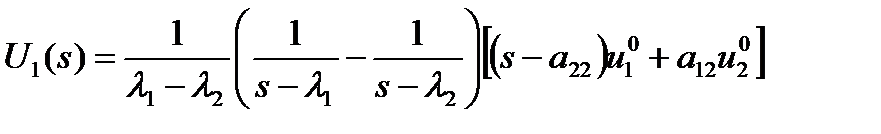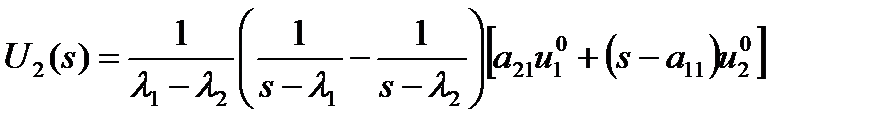Поскольку согласно табл. 1.1 прообразом 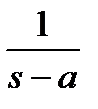служит 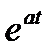, а прообразом

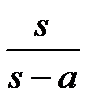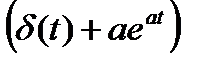— ,то получаем

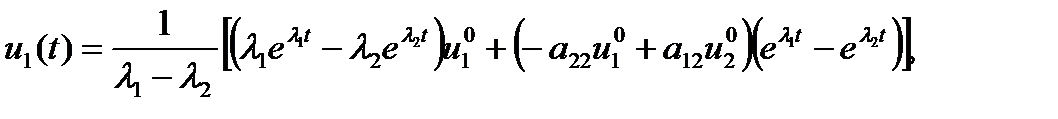(1.5.25)

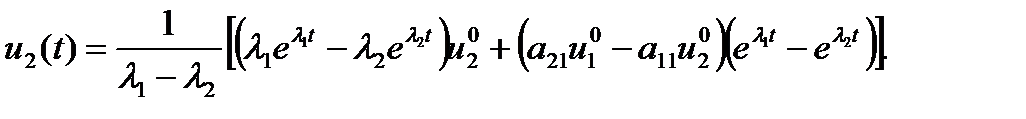
Как видно из полученного решения, при ,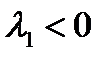

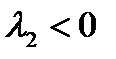
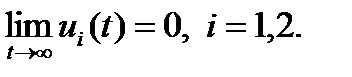
Напротив, если хотя бы один из корней положителен, то имеет ме­сто неограниченное возрастание (убывание) 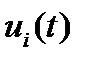при (), .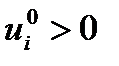

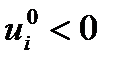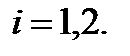Если же 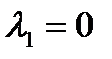, то система после экспоненциально затухающего переходного процесса перейдет в новое установившееся состояние

,

.

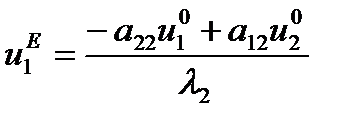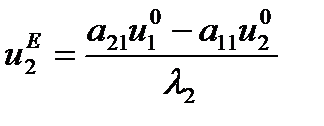Поведение системы пр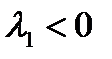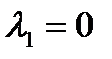и , и 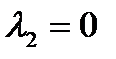показано на рис. 1.22.

Снова вернемся к содержательной интерпретации условий воз­никновения рассматриваемой ситуации. Основное условие — поло­жительность дискриминанта, т.е. выполнение неравенства

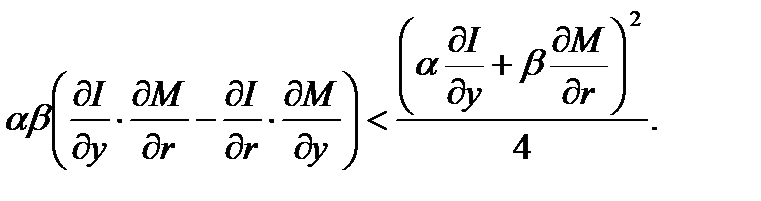
Последнее неравенство эквивалентно следующему (в круглые скобки взяты заведомо положительные величины):

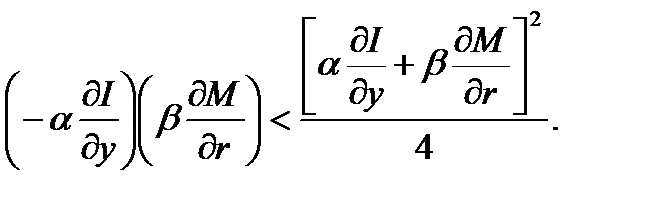(1.5.26)

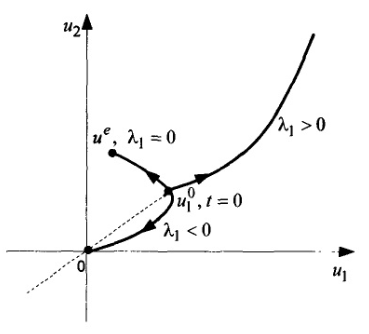
Рис. 1.22, Фазовые траектории системы при действительных корнях характеристического уравнения

Неравенство (1.5.26) будет выполняться, по крайней мере, в том случае, когда

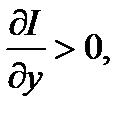
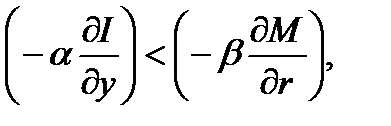
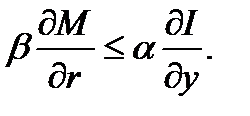(1.5.27)

что возможно.

Корень 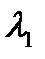отрицателен, по крайней мере, тогда, когда производная 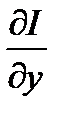становится пренебрежимо малой, но оставаясь положительной. Отрицательность 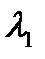следует при этом из неравенства (в круглых скобках заведомо положительные величины):

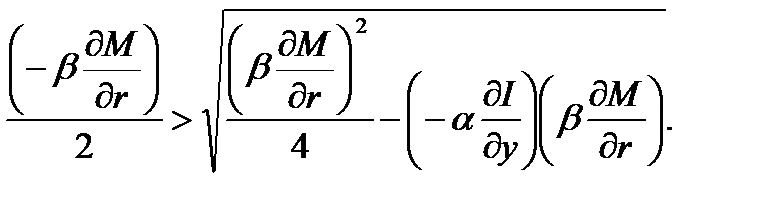
Выводы. Подведем итоги. Нелинейная динамическая система (1.5.9) имеет точку равновесия 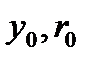,являющуюся решением сис­темы из двух нелинейных алгебраических уравнений:

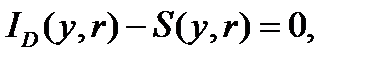
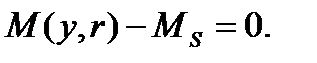
В результате некоторого импульсного воздействия система была «выбита» из состояния равновесия 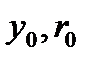в некоторое другое состояние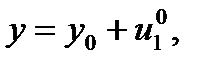 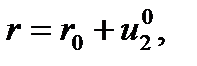находящееся в окрестности равновесного состояния.

Для изучения дальнейшего поведения системы (1.5.9) она была линеаризована, т.е. заменена приближенно линейным аналогом (1.5.15) — линейной двухсвязной системой, в которой

, , , .

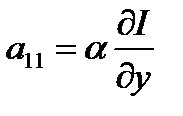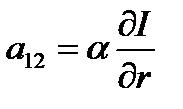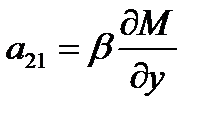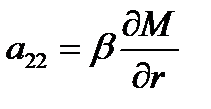Поведение линеаризованной системы определяется типом кор­ней характеристического уравнения

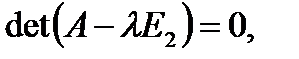
которое является квадратным алгебраическим уравнением:

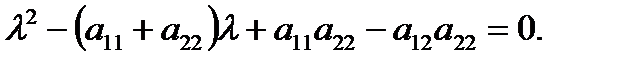
Если корни чисто мнимые 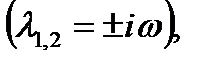то система находится в незатухающих автоколебаниях с круговой частотой 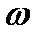, при этом ее координаты 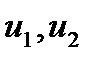описывают замкнутый цикл, проходящий через начальную точку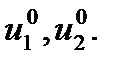

Если корни комплексные взаимно сопряженные 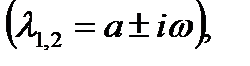то при а < 0 система находится в затухающих автоколебаниях и воз­вращается в точку покоя 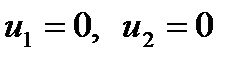. При а >0 система находится в автоколебательном режиме с экспоненциально возрастающей амплитудой.

Если корни действительные 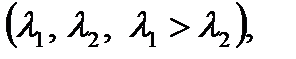то при 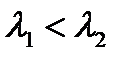система из начального состояния 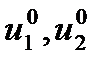возвращается в состояние покоя 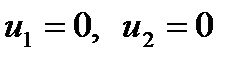. При 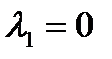система постепенно переходит в новое состояние покоя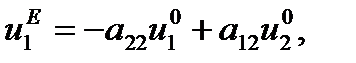 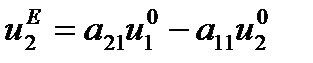. При 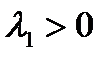система неограниченно удаляется от начального состояния .

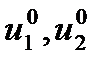Поскольку

,, , .

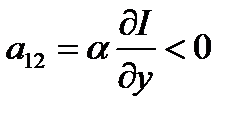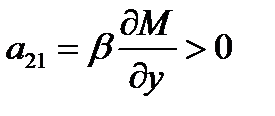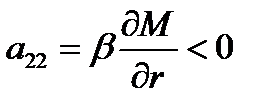то варианты поведения реальной системы охватывают лишь часть вариантов поведения линейной двухсвязной системы, однако было показано, что возможна реализация всех описанных типов поведения.

Дата добавления: 2015-06-04