Решение однородного уравнения

Однородное уравнение имеет вид:

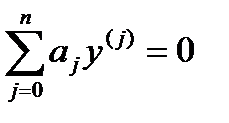. (П.1.2)

Прямой проверкой убеждаемся, что является решением однородного уравнения (П.1.2):

.

если (ведь ) удовлетворяет уравнению:

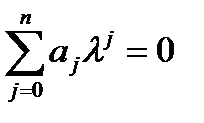. (П.1.3)

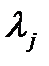Уравнение (П.1.3) называется характеристическим. Поскольку любой полином n-й степени имеет п корней, то характеристическое уравнение имеет п корней и каждому корню отве­чает решение .

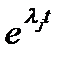Если корень имеет кратность , то наряду с 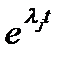решениями также являются 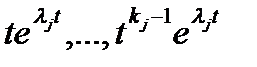(доказывается простой провер­кой). Решения, отвечающие кратному корню, линейно независимы.

Если корень 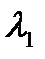является комплексным (перенумеруем корни так, чтобы этот корень стал первым), то обязательно есть корень, сопряженный с ним (перенумеруем корни так, чтобы сопряженный корень стал вторым):

,

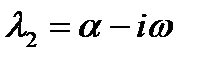
Следовательно, решения являются комплексными

, ,

поэтому заменяем их на действительные

,

.

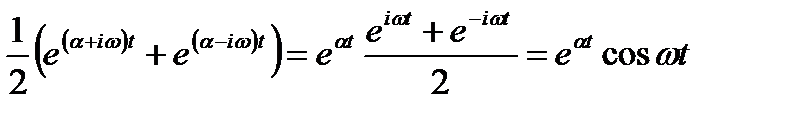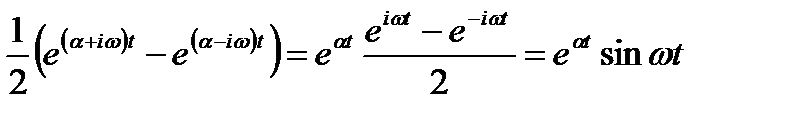Эти два решения линейно независимы, поскольку независимы , .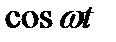

При разных данные решения линейно независимы, поэтому они образуют фундаментальную систему решений однородного урав­нения. Итак, общее решение однородного уравнения имеет вид:

(П.1.4)

(чтобы не загромождать выражение, написали его в предположе­нии, что кратных корней нет, а первые 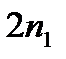корней — комплексные взаимно сопряженные).

Дата добавления: 2015-06-04