Управление динамическими системами

Под управлением понимается прямое воздействие на систему, направ­ленное на достижение заданного результата.

В этом заключается основное отличие управления от регулиро­вания, которое осуществляется на основе сравнения регулируемого (выходного) показателя с задающим (входным).

Под оптимальным управлением понимается выбор из множества возможных такого варианта управления, который по заданному крите­рию является оптимальным.

Выше последовательно были исследованы все более усложняю­щиеся системы от линейных односвязных до нелинейных много­связных. Как видно из этого исследования, поведение любой нели­нейной многосвязной системы описывается следующими уравне­ниями движения:

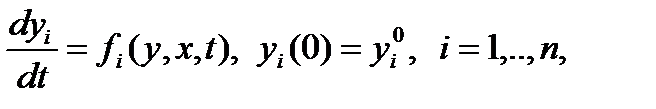(1.6.1)

где у — вектор фазовых координат, задающий состояние системы;

x — вектор внешних (входных) задающих и (или) возмущающих

воздействий на систему;

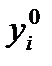— начальные значения фазовых переменных.

Если возмущающие воздействия пренебрежимо малы, некото­рые из задающих воздействий становятся управляющими, а некото­рые являются заданными известными функциями времени, то при­ходим к следующим уравнениям для управляемой динамической системы:

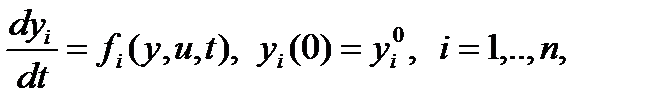(1.6.2)

где и — вектор управляющих параметров, ;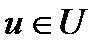

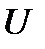— область допустимых значений управляющих параметров.

Управляющая траектория (управление) 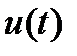называется допусти­мой, если она кусочно-непрерывна и в точках разрыва непрерывна слева:

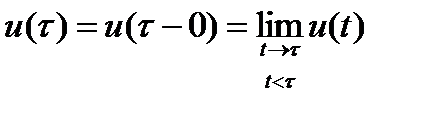
и, кроме того, при любом .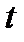

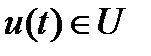Если задан закон управления, т.е. определена допустимая управ­ляющая траектория 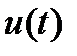, то уравнения для фазовых переменных принимают вид:

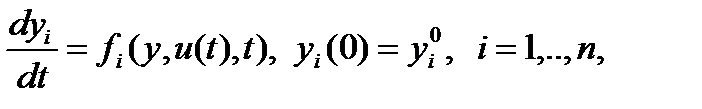(1.6.3)

тем самым при любых начальных условиях 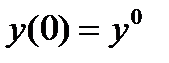однозначно оп­ределяется решение.

В качестве критерия оптимальности выбирается некоторый функ­ционал от фазовой и управляющей траекторий, который подлежит максимизации (минимизации):

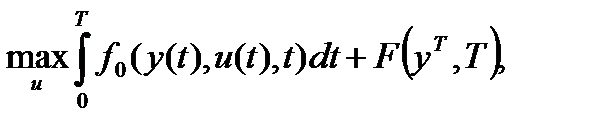(1.6.4)

где 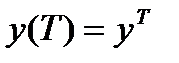— возможное конечное значение вектора состояния.

Согласно принципу максимума Понтрягина, описанному в При­ложении 3, алгоритм нахождения оптимального решения задачи (1.6.3), (1.6.4) заключается в следующем.

1. Для каждого уравнения движения (1.6.3) вводится двойствен­ная (сопряженная) переменная .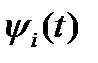

2. Строится функция Гамильтона (гамильтониан):

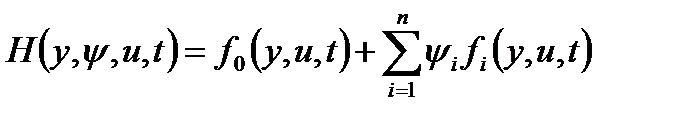, (1.6.5)

3. Формируются уравнения для сопряженных переменных:

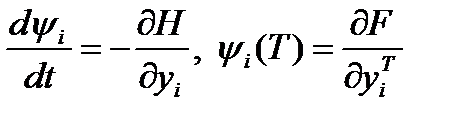, (1.6.6)

4. При фиксированных y_t у, г определяются значения управ­ляющих параметров, доставляющих максимум гамильтониану:

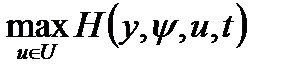(1.6.7)

5. Из участков уравнений 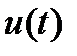,удовлетворяющих при каждом соотношению (1.6.7), формируется оптимальная управляющая траек­тория .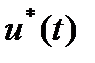

Дата добавления: 2015-06-04