Нелинейная динамическая система

Экономика в форме модели Солоу как односвязная

Снова вернемся к рассмотрению модели Солоу, поскольку она выполняет роль базовой. Напомним, что в абсолютных показателях эта модель имеет вид:

где у — ВВП;

I — инвестиции;

С — фонд потребления;

K — ОПФ;

L — число занятых;

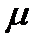— коэффициент износа;

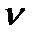— темп прироста числа занятых.

Структурная схема этой модели уже приводилась в § 1.1. На рис. 1.23 представим ее в следующем виде.

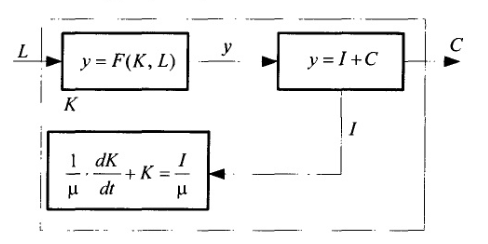
Рис. 1.23. Структурная схема модели Солоу

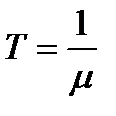Из рис. 1.23 видно, что входом в систему служит число занятых L, выходом — фонд потребления C, поэтому данная система односвязная, В структуре системы имеется контур обратной связи, кото­рый образуется из нелинейного статического элемента y=F(K, L), распределительного линейного статического звена y=I +С и инерционного звена , где . Поскольку в системе имеется нелинейный элементу y =F(K, L), то система нелинейна.

Роль регулятора в контуре обратной связи выполняет распреде­лительное звено y=I + С. Обычно изучается такое долгосрочное регулирование, при котором соотношение между потреблением и накоплением постоянно. При этом

,

где ρ— норма накопления.

В качестве альтернативного варианта рассмотрим регулирование с постоянными инвестициями I. Пусть в начальный момент t =0 система находилась в состоянии равновесия при инвестициях I ₀. Тогда установившееся решение инерционного звена 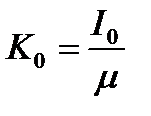, поэтому , .

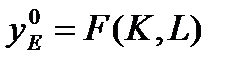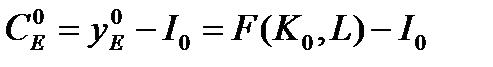При постоянных инвестициях I ₀ имеет место экстенсивный рост ВВП 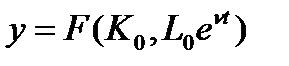за счет роста числа занятых . Фонд потребления также растет:

.

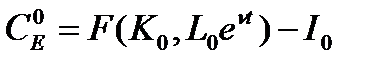Однако при этом фондовооруженность сокращается:

, ,

а удельное потребление (в расчете на одного занятого) вначале рас­тет, а затем сокращается. В самом деле, если — линейно-однородная функция, то удельное потребление равно:

,

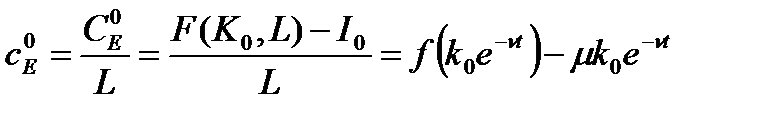где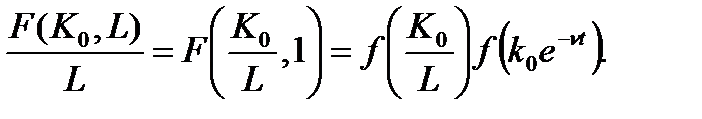

Поскольку производная (при )

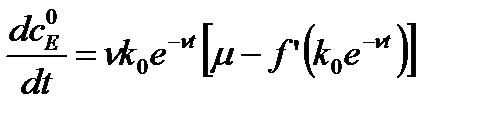
в нуле положительна 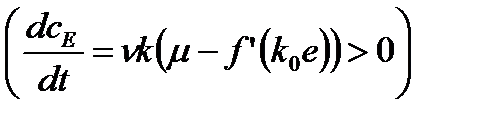, а для достаточно больших 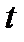отрицательна 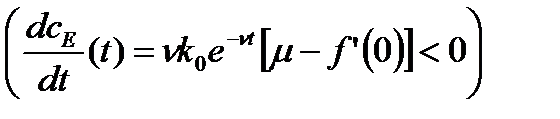, то в некоторый момент производная обратится в нуль:

.

Таким образом, при удельное потребление начинает убы­вать. Поэтому возникает необходимость увеличить инвестиции с I ₀ до некоторого нового значения 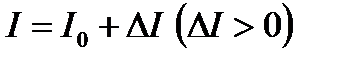. Предположим, что такое увеличение инвестиций произошло. Как с этого момента, который примем за новое начало отсчета времени, изменится пове­дение системы?

Поскольку ОПФ удовлетворяют уравнению инерционного звена

, ,

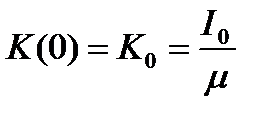то как решение этого уравнения (которое было получено и иссле­довано в § 1.2) фонды будут изменяться следующим образом:

,

.

Поэтому ВВП как функция ОПФ и числа занятых

будет возрастать за счет роста как фондов, так и числа занятых. По достижении фондами установившего значения 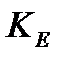рост ВВП про­должится только за счет роста числа занятых:

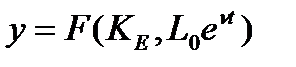
После этого по отмеченным выше соображениям (падение фондовооруженности и удельного потребления) через некоторое время снова потребуется увеличить ежегодные инвестиции.

Интересно отметить, что при рассмотренном варианте регули­рования в течение всего переходного процесса норма накопления убывает:

,

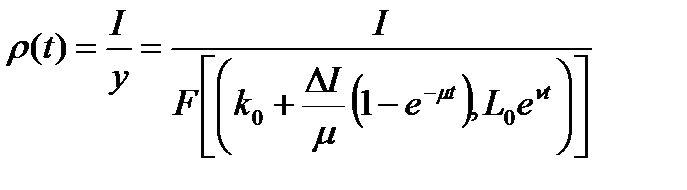поскольку числитель постоянен, а знаменатель растет.

Дата добавления: 2015-06-04