Экономика в форме односекторной модели оптимального роста как управляемая система

Односекторная модель экономического роста (модель Солоу), рассмотренная в § 1.1, в абсолютных показателях имеет вид:

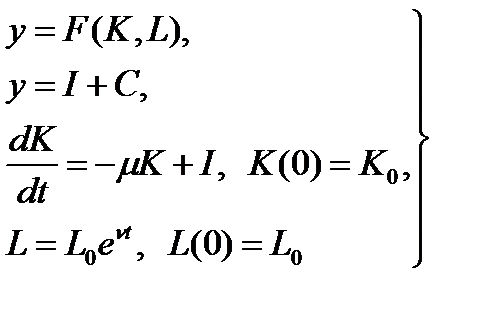(1.6.8)

В этой модели:

Y — ВВП;

K — ОПФ;

L — число занятых;

I — инвестиции;

С — фонд непроизводственного потребления;

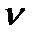— темп прироста числа занятых;

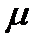— коэффициент износа (выбытия) ОПФ.

Переменные Y, I, С, K, L являются эндогенными (определяемыми внутри модели), коэффициенты 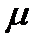, 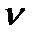— экзогенными (задаваемыми извне модели).

В удельных показателях (в расчете на одного занятого) данная модель принимает вид:

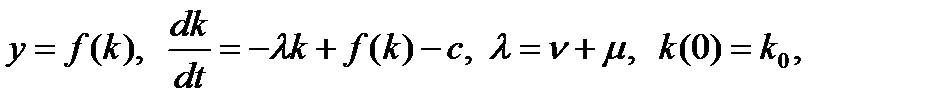
где 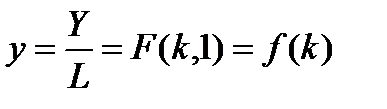— ВВП в расчете на одного занятого;

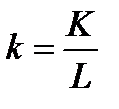— фондовооруженность;

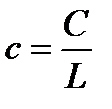— непроизводственное потребление в расчете на одного,занятого

(удельное потребление).

Предположим теперь, что можно управлять удельным потребле­нием с целью максимизировать интегральное удельное дисконтиро­ванное потребление за длительный промежуток времени:

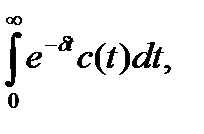
где 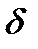— коэффициент дисконтирования.

В этот интеграл будущие значения удельного потребления вхо­дят с экспоненциально убывающим весом.

Таким образом, приходим к следующей модели оптимального

роста:

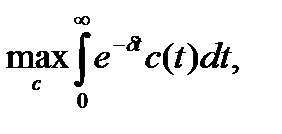(1.6.9)

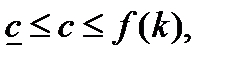(1.6.10)

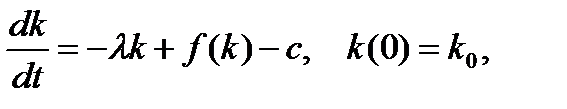(1.6.11)

В этой задаче выражение (1.6.9) задает критерий, (1.6.10) — об­ласть допустимых значений управляющего параметра ( 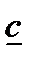—минимально допустимое с социальной точки зрения значение удельного потребления), (1.6.11) — уравнение для единственной фазовой пе­ременной k. Решением данной задачи служит оптимальная допус­тимая траектория удельного потребления 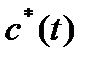, доставляющая мак­симум функционалу (1.6.9), и соответствующие ей оптимальные траектории фондовооруженности и удельного ВВП 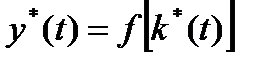. Вместе 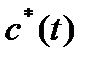, и 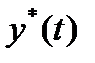составляют траекторию оп­тимального экономического роста.

В соответствии с алгоритмом принципа максимума Понтрягина вводим одну сопряженную переменную 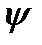(поскольку только одна фазовая переменная 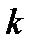)и строим гамильтониан:

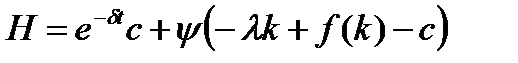. (1.6.12)

Уравнение для сопряженной переменной имеет вид

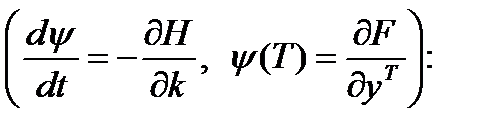
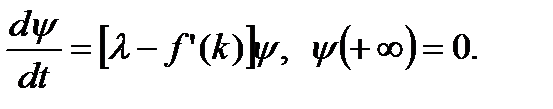
Сопряженную переменную 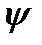удобнее представить в виде ,

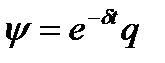поэтому 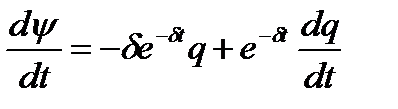и для q получаем следующее уравнение:

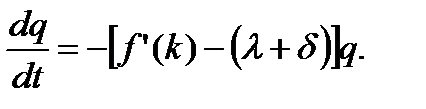(1.6.13)

Поскольку общее решение уравнения (1.6.1З) имеет вид: 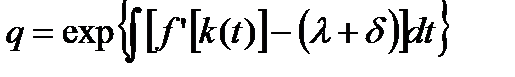, то q >0. Теперь надо максимизировать гамильтониан:

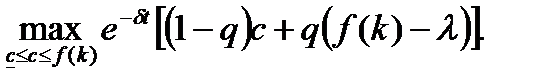
Поскольку, как видно из последнего выражения, гамильтониан линейно зависит от c с коэффициентом (1- q), то его максимум достигается на концах отрезка 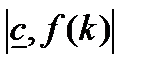при 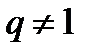и в некоторой промежуточной точке при q =1, тем

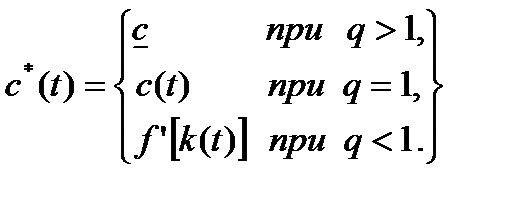(1.6.14)

При уточнении оптимального правила (1.6.14) необходимо при­нимать во внимание, что k и q удовлетворяют уравнениям (1.6.11) и (1.6.13), т.е. участки этих траекторий-решений участвуют в образо­вании правила (1.6.14).

Уравнения (1.6.11) и (1.6.13) имеют следующие стационарные решения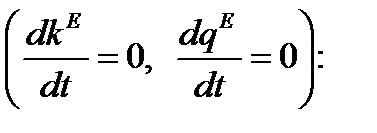

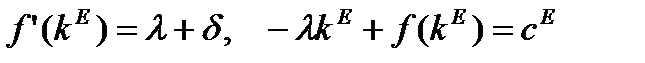(1.6.15)

В частности, q =1 является стационарным решением уравнения (1.6.13), поэтому при q= 1 выполняется (1.6.15). Таким образом, оптимальное правило приобретает следующий вид:

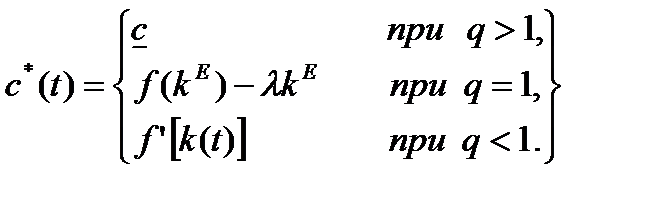(1.6.16)

Исследуем теперь оптимальные траектории фазовой и сопря­женной переменных , 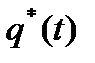в предположении .

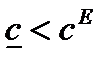1. Вначале рассмотрим область q >1. В этой области 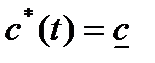, поэтому уравнение для фазовой переменной принимает вид:

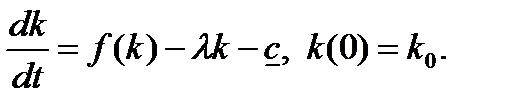(1.6.17)

Обозначим через 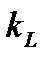меньший корень уравнения

,

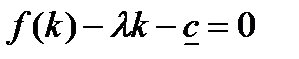графическое решение которого показано на рис. 1.24.

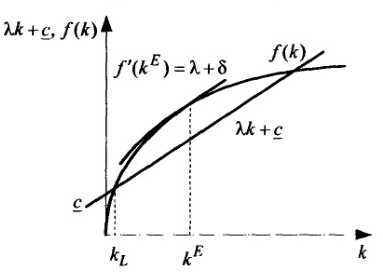
Рис. 1.24.

Поскольку 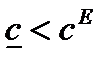, 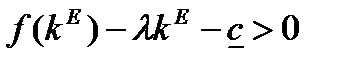то тем самым 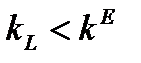поэтому при 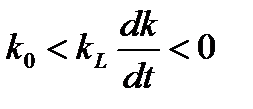, т.е. фондовооруженность убывает и удаляется от стационарного значения. Напротив, при 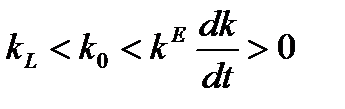, и фондовооруженность возрастает, оставаясь левее стационарного значения 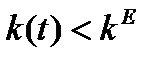. Поскольку 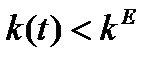, то согласно (1.6.13) , тем самым q> 1 и непрерывно убывает, поэтому наступит такой момент 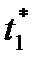, для которого 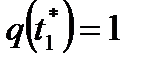,при этом , .

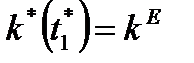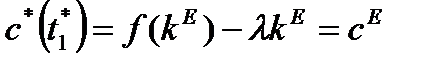Если же 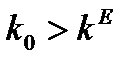, то согласно (1.6.13) 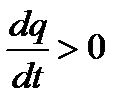и q(t) удаляется от стационарного значения .

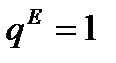2. Теперь рассмотрим область q <1. В этом случае , т.е. на потребление работают все фонды (нет ни расширения, ни даже восстановления фондов), поэтому уравнение для фазовой пе­ременной примет вид:

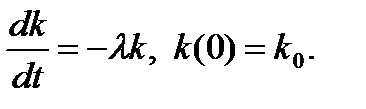
Решение последнего уравнения —

.

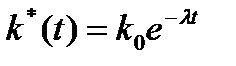Если 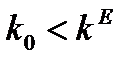, то нет сходимости к стационарному значению 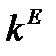. При 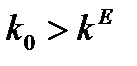фондовооруженность, убывая, в некоторый момент 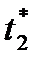достигнет стационарного значения :

,

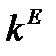при этом .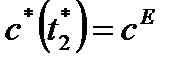

На рис. 1.25, 1.26 показаны оптимальные траектории фондовооруженности и удельного потребления для тех случаев, когда имеет место сходимость к стационарным траекториям (верхний индекс (1) соответствует области q > 1, верхний индекс (2) — области q < 1).

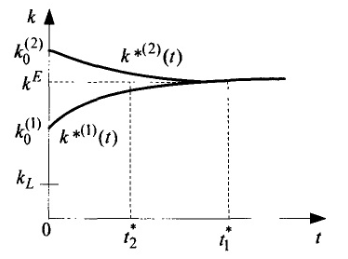
Рис. 1.25. Оптимальные траектории фондовооруженности

Таким образом, получаем следующую картину оптимального управления. При q >1, 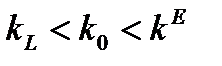фондовооруженность непрерыв­но растет за счет того, что удельное потребление удерживается на предельно низком уровне. Как только в момент 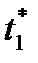фондовооруженность достигает стационарного значения, система переходит на ста­ционарный режим: имеет место такое воспроизводство, которое по­зволяет поддерживать фондовооруженность на стационарном уровне 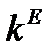, удельное потребление постоянно равно , .

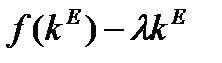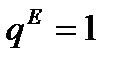При q< 1, 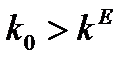в фонды не поступает никаких вложений, поэтому фондовооруженность сокращается за счет увеличения чис­ла занятых по закону 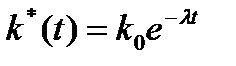, , 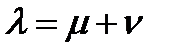потребление также сокращается по закону 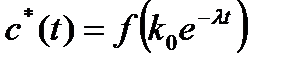, пока фондовооруженность не достигнет в момент стационарного значения 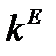, после чего система входит в стационарный режим. Во всех остальных случаях система не достигает стационарного режима.

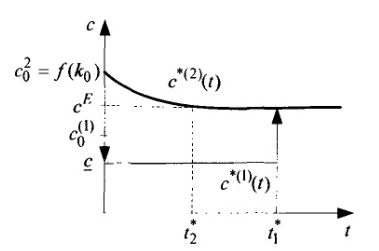
Рис. 1.26. Оптимальные траектории удельного потребления

Оптимальный рост замкнутой трехсекторной экономики, описы­ваемой в следующем разделе, представлен в Приложении 3.

Вопросы и задания

1. Что такое динамический элемент и динамическая система?

2. Почему экономика является динамической системой?

3. В чем сходство и различие понятий: «мультипликатор», «акселе­ратор», «инерционное звено», «колебательное звено»? Где эти по­нятия используются в экономике?

4. Что такое импульсная функция? Какова импульсная функция инерционного звена?

5. Что такое переходная функция? Какова переходная функция инерционного звена?

6. Какова переходная функция колебательного звена?

7. Как среагирует экономика в форме упрощенной модели Кейнса

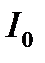, на увеличение ежегодных инвестиции с до 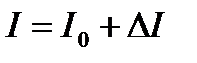? Каков экономический смысл коэффициентов дан­ной модели?

8. Как среагирует экономика в форме модели Самуэльсона—Хикса

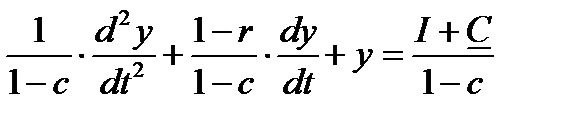на увеличение ежегодных инвестиций с 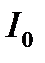до 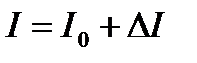? Каков экономический смысл коэф­фициентов данной модели?

9. Как изменится реакция экономики в форме динамической моде­ли Кеинса на изменение величины ежегодных инвестиций с 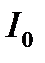до 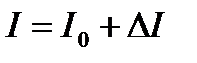при введении мультипликатора в контур обратной свя­зи с данной моделью?

10. Как изменится реакция экономики в форме динамической моде­ли Кеинса на изменение величины ежегодных инвестиций с 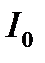до 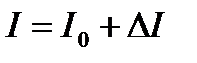при введении акселератора в контур обратной связи с этой моделью?

11. Что такое передаточная функция?

12. Каковы передаточные функции мультипликатора, акселератора, упрощенной модели Кейнса, модели Самуэльсона—Хикса?

13. Как найти передаточную функцию последовательного (параллельного) соединения, контура с обратной связью по передаточным функциям составляющих их элементов?

14. В каких соотношениях находятся импульсная и переходная функ­ции с передаточной функцией?

15. Какая линейная динамическая система является устойчивой?

16. Устойчива ли экономика в форме упрошенной модели Кейнса?

17. Устойчива ли экономика в форме модели Самуэльсона—Хикса?

18. Что такое многосвязная динамическая система?

19. Можно ли говорить о передаточной функции нелинейной системы?

БИБЛИОГРАФИЧЕСКИЙ

СПИСОК

1. Занг В.-Б. Синергетическая экономика. — М.; Мир, 1999.

2. Петровский И.Г. Лекции по теории обыкновенных дифференциаль­ных уравнений. — 7-е изд. — М.; Физматгиз, 1987,

3. Колемаев В.А. Математическая экономика: Учебник. — 2-е изд. - М.: ЮНИТИ-ДАНА, 2002.

ПРИЛОЖЕНИЯ

Приложение 1

Справочные сведения о линейных дифференциальных

уравнениях и системах линейных дифференциальных

уравнений с постоянными коэффициентами

Линейным уравнением п-го порядка называется уравнение вида

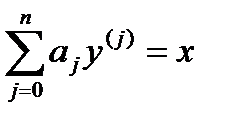, (П.1.1)

где ,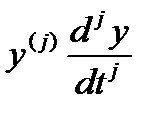

x=x (t) — некоторая известная функция времени (правая часть уравнения).

Если коэффициенты уравнения 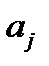не зависят от времени, то уравнение (П.1.1) называется уравнением с постоянными коэффици­ентами. Линейное уравнение называется однородным, если x= 0, и неоднородным в противном случае.

Система решений 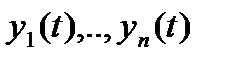однородного линейного уравне­ния называется фундаментальной, если эти функции линейно незави­симы на рассматриваемом временном интервале.

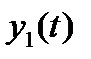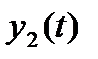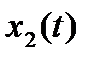Если и являются решениями уравнения (П.1.1) с пра­выми частями и то 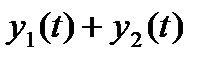является решением этого уравнения с правой частью 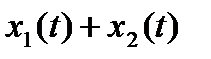. Поэтому для получения общего решения неоднородного уравнения надо к общему решению однородного уравнения добавить любое частное решение неодно­родного.

Дата добавления: 2015-06-04