Операторный метод решения линейных дифференциальных уравнений с постоянными коэффициентами

Общее и конкретное решение неоднородного уравнения

Добавив к общему решению однородного уравнения любое частное решение неоднородного уравнения 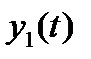, получаем общее решение неоднородного уравнения . Если заданы начальные условия , , 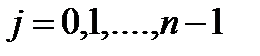то однозначно оп­ределяются константы общего решения, тем самым находится единственное конкретное решение для данных начальных условий.

Частное решение определяется методом вариации постоянных, методом Коши или операторным методом.

Операторный метод основан на использовании преобразований Лапласа входящих в уравнение функций времени.

Преобразованием Лапласа некоторой функции 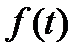называется следую­щий интеграл от функции , зависящий, вообще говоря, от ком­плексного параметра s:

, (П.1.5)

где F(s) — образ функции (прообраза) .

Преобразование Лапласа осуществляет отображение временного пространства (пространства функций времени) в пространство об­разов или частотное пространство.

Для обратного преобразования из частотного пространства во временное справедливо выражение

, (П.1.6)

— параметр преобразования Лапласа;

— параметр затухания;

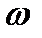— круговая частота, .

Преобразование функции и ее производной связаны следующим образом (интегрируем по частям):

,

тем самым

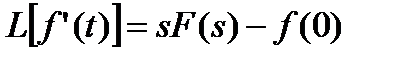. (П.1.7)

Если , то операции дифференцирования по времени во временном пространстве соответствует операция умножения на s в пространстве образов.

Применив преобразование Лапласа к уравнению (П.1.1) с по­стоянными коэффициентами и при нулевых начальных условиях, по­лучим следующее алгебраическое уравнение:

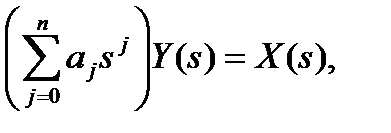(П.1.8)

где , .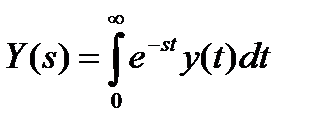

Из (П.1.8) можно найти образ решения

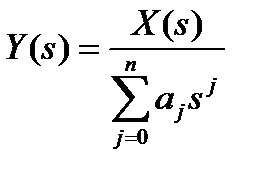(П.1.9)

как частное от деления образа правой части на характеристический многочлен уравнения, в который вместо 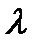подставлен параметр преобразования s.

Зная образ решения , можно найти само решение 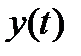либо непосредственно по формуле обратного преобразования (П.1.6), ли­бо по таблице преобразований Лапласа (табл. 1.1 преобразований Лапласа от некоторых наиболее употребляемых в макроэкономических исследованиях функций).

Дата добавления: 2015-06-04