Линейные многоснязные динамические системы. Динамическая модель Леонтьева

Многосвязной называется такая динамическая система, состояние ко­торой задается не одной» а многими выходными (фазовыми) пере­менными при этом все они взаимно связаны друг с дру­гом.

Многосвязная система линейна, если производная любой фазо­вой переменной линейно зависит от фазовых переменных:

, , , (1.4.1)

где — входное воздействие на i -ю фазовуюпеременную.

Любая односвязная линейная система может быть представлена в форме линейной многосвязной системы. Например, линейный динамический элемент n -го порядка, заданный уравнением

, , ,

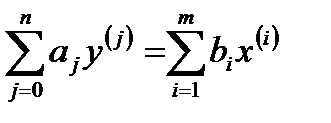представляется в форме следующей линейной многосвязной систе­мы (относительно п фазовых переменных , , ,.., ):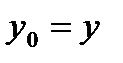

,

,

…

,

,

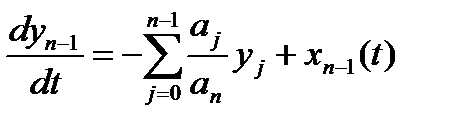где .

В матричном виде система уравнений (1.4.1) может быть запи­сана в следующем виде:

, , (1.4.2)

где , , , , .

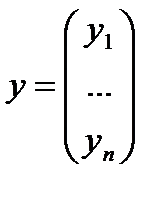Поскольку рассматриваемые системы, задаваемые уравнениями (1.4.1) или (1.4.2), линейны, то к их исследованию может быть применен математический аппарат, аналогичный использованному для односвязных линейных систем.

В частности, если применить преобразование Лапласа к обеим частям матричного уравнения (1.4.2), то получим (напомним, что ):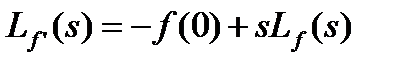

.

Если начальные условия нулевые, т.е. , то

, (1.4.3)

откуда

,

или в развернутом виде:

,

где 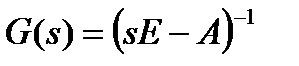— передаточная функция ( вформе матрицы)

многосвязной системы,

Таким образом, найдя преобразование Лапласа от всех компо­нент входного вектора 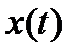, умножаем их затем на элементы i -й строки передаточной матрицы и складываем произведения, что дает в итоге образ i -й фазовой переменной. Осталось прибегнуть к таб­лице преобразований Лапласа, чтобы получить прообраз , т.е. траекторию любой i -й фазовой переменной, а в итоге и всю траек­торию системы при заданном входном воздействии .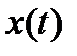

В передаточной матрице 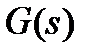внедиагональные элементы выражают перекрестные влияния фазовых переменных друг на друга. Если бы все внедиагональные элементы были равны нулю (т.е. , ) то имело бы смысл изучать порознь п односвяз-ных линейных систем с передаточными функциями .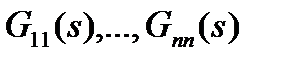

При переходе к многосвязным линейным системам все приемы анализа и синтеза систем, примененные для односвязных линейных систем, остаются в силе.

Многосвязная линейная система, как и односвязная, устойчива, если ее реакция на импульсное воздействие в форме функции Ди­рака затухает.

Импульсное воздействие на систему выводит ее из состояния покоя, после чего система (в случае устойчивости) должна возвра­титься в состояние покоя. Исследование устойчивости сводится к исследованию поведения системы однородных дифференциальных уравнений при ненулевых начальных условиях (результат импульсного воздействия):

, . (1.4.4)

Согласно Приложению 1, общее решение однородного уравне­ния (1.4.4) имеет вид:

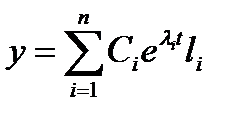, (1.4.5)

где , i = 1,.., п — общие константы решения, которые для конкретного

решения определяются на основе п начальных усло­вий

, ;

, i = 1,..., п — корни характеристического уравнения

, (1.4.6)

, i = 1,..., п — нормированные собственные векторы матрицы А,

соответствующие ее собственным числам (корням

харак­теристического уравнения), т.е, каждый вектор

явля­ется решением системы .

Следует заметить, что форма общего решения (1.4.5) имеет силу для разных характеристических корней. Если же некоторые из них кратные, то надо внести изменения, указанные в Приложении 1.

Как видно из (1.4.5), достаточным условием устойчивости ли­нейной многосвязной системы является отрицательность действи­тельных характеристических корней.

Дата добавления: 2015-06-04