Экономика в форме динамического межотраслевого баланса как многосвязная линейная динамическая система

Статический межотраслевой баланс Леонтьева получается приравниванием чистых выпусков отраслей конечному спросу на про­дукцию отраслей¹:

, (1.4.7)

где 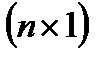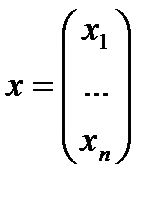— вектор-столбец годовых валовых выпусков отраслей;

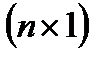
— вектор-столбец годового конечного спроса на

продукцию отраслей;

— матрица прямых затрат, каждый элемент которой

показывает, сколько единиц продукта i необходимо для

производства единицы j -го продукта. При этом

предполагается, что не зависят от времени и

масштаба производства.

Если теперь вектор конечных продуктов в каждый год t пред­ставить в виде двух векторов: инвестиционных товаров (продуктов) и потребительских товаров, то получим модель динамического межотраслевого баланса:

¹ Обозначения использованы такие, какие сложились в этой сфере экономической науки.

, t =1,2,… (1.4.8)

где В— матрица приростных фондоемкостей, каждый элемент которой

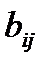показывает, сколько единиц продукта i необходимо

произвести для увеличения годового производства j -го

продукта на единицу;

— вектор-столбец конечного (непроизводственного) потребления.

С экономической точки зрения соотношение (1.4.8) показывает разделение вектора валовых выпусков (а следовательно, и каждый его компоненты) на т р и части:

1) Ах_t, — текущее производственное потребление, включая

амортизацию;

2) — капитальные затраты на расширение производства;

3) — конечное (непроизводственное) потребление.

Модель (1.4.7) с дискретным временем можно преобразовать в мо­дель с непрерывным временем следующим образом:

,

,

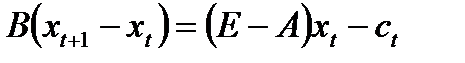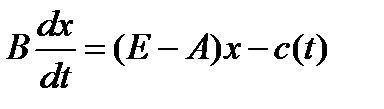. (1.4.9)

Если обратная матрица B ^-1 существует, то модель (1.4.9) может быть приведена к виду:

, , (1.4.10)

т.е. к форме линейной многосвязной системы, входом в которую служит вектор конечного производственного потребления , а вы­ходом — вектор валовых выпусков .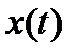

Таким образом, для устойчивости экономики в форме динамиче­ского межотраслевого баланса достаточно (см. (1.4.6)), чтобы корни характеристического уравнения

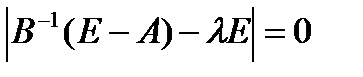(1.4.11)

имели отрицательные действительные части.

Например, при п = 1 соотношение (1.4.11) принимает вид:

,

где а — доляпро межуточного продукта в валовом выпуске;

b — приростная фондоемкость валового выпуска,

поэтому , т.е. экономика неустойчива и может, вообще говоря, неограниченно наращивать валовой выпуск.

Подобная картина имеет место и при п > 1, поэтому в модели баланса обязательно присутствуют ограничивающие факторы, кото­рые действуют в реальной экономике. Это прежде всего ограничен­ные трудовые ресурсы. Если известна траектория трудовых ресурсов L(t), то текущий выпуск ограничен:

,

где l = (l ₁,.,., l_п) — вектор-строка отраслевых трудоемкостей.

Кроме того, другим ограничивающим фактором являются при­родные ресурсы, добыча и вовлечение которых в производственный оборот по мере исчерпания наиболее экономически эффективной их части становятся все более затруднительными и менее эффек­тивными.

Дата добавления: 2015-06-04