Выполнения заданий. Теоретические вопросы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ

Теоретические вопросы

1. Матрицы. Основные понятия.

2. Действия над матрицами.

3. Определители. Свойства определителей.

4. Обратная матрица.

5. Решение систем линейных уравнений. Формулы Крамера.

6. Решение систем линейных уравнений методом Гаусса.

7. Теорема Кронекера – Капелли..

8. Основные свойства определенного интеграла.

9. Матричная запись систем линейных уравнений.

Пример 1 (Метод Крамера):

С помощью определителей решить систему уравнений

Решение: Найдем определитель системы

.

– система имеет единственное решение.

Дополнительные определители получают, заменив столбец коэффициентов при неизвестном свободными членами.

,

.

; ; .

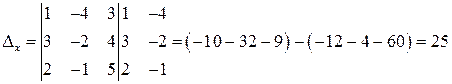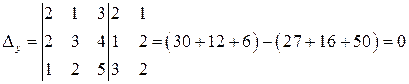
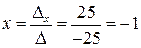Ответ: (-1;0;1)

Пример 2 (Метод Гаусса): Решить систему уравнений методом последовательного исключения неизвестных.

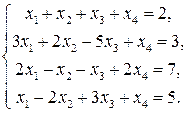
Решение:

Стрелочками укажем действия над данной строкой уравнения и место записи результата этого действия

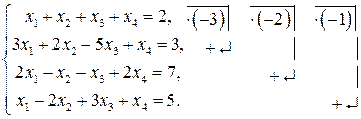
Разделим последнюю и предпоследнюю строки на 2; поменяем столбцы при и .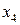

Ответ:

Пример 3: Решить систему уравнений средствами матричного исчисления.

Решение:

Представим систему в матричном виде: , где , ,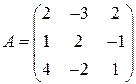

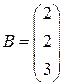
Тогда 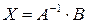. Это матичная запись решения системы линейных уравнений. Таким образом, чтобы решить систему линейных уравнений надо:

1) составить матрицу , обратную матрицы системы ;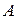

2) умножить матрицу слева на матрицу-столбец свободных членов ;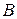

В результате этого мы получим столбец – решение системы.

Составим обратную матрицу для матрицы A.

1. Существует ли для матрицы 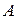обратная матрица ?

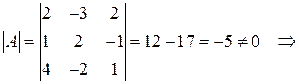
матрица 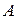невырожденная (), следовательно, обратная матрица существует.

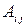2. Для нахождения транспонированной матрицы алгебраических дополнений счет элементов будем вести в том порядке, как это указанно в формуле .

, ,

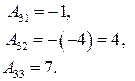
Получим:

- обратная матрица.

Применив 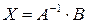, получим

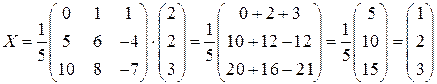
Ответ: .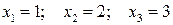

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

а). Решить систему уравнений методом Крамера и с помощью обратной матрицы.

б). Решить систему уравнений методом Гаусса.

1. а)	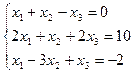б)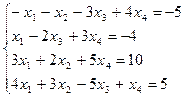
2. а)	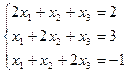б)
3. а)	б)
4. а)	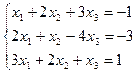б)
5. а)	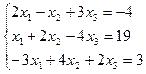б)
6. а)	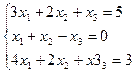б)
7. а)	б)
8. а)	б)
9. а)	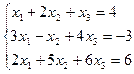б)
10. а)	б)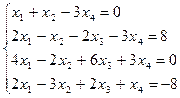
11. а)	б)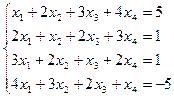
12. а)	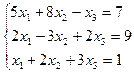б)
13. а)	б)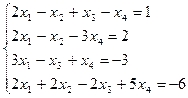
14. а)	б)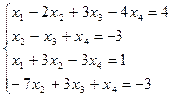
15. а)	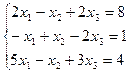б)
16. а)	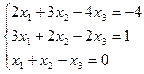б)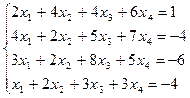
17. а)	б)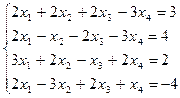
18. а)	б)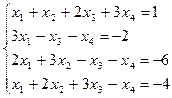
19. а)	б)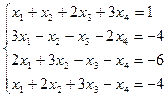
20. а)	б)
21. а)	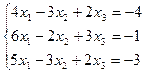б)
22. а)	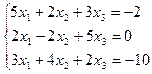б)
23. а)	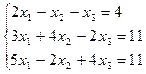б)
24. а)	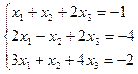б)
25. а)	б)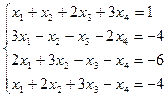
26. а)	б)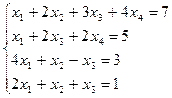
27. а)	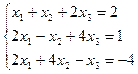б)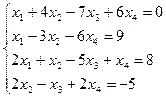
28. а)	б)
29. а)	б)
30. а)	б)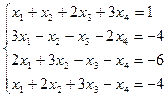

Дата добавления: 2015-07-02