Функционалы, зависящие от высших порядков

Условия закрепления y(х)

y(x₁) = y₁ y^(n-1)(x₁) = y₁^(n-1)

y(x₂) = y₂ y^(n-1)(x₂) = y₂^(n-1)

y^(n-2)(x₁) = y₁^(n-2)

y^(n-2)(x₂) = y₂^(n-2)

=

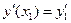
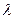- вещественный множитель

Находим то, что содержит 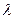, дифференцируем по промежуточному аргументу, а затем по основному.

=

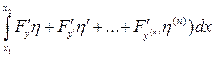
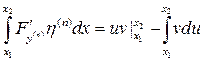
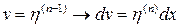
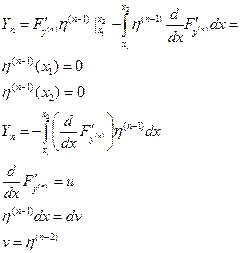
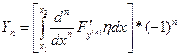
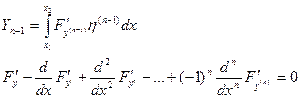
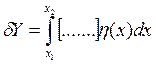
Лекция №8

Функционалы, зависящие от нескольких аргументов (векторного аргумента)

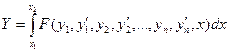
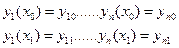
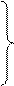выборочное производство: y₁,y_2,...,y_n

должны 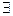производные много 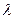(n штук)

но так нельзя!

Функционал зависит от одного аргумента

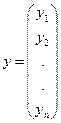
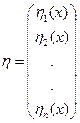
Вводим только 1 значение :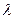

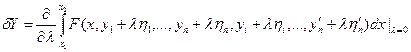
Функционал, зависящий от одного векторного аргумента

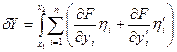- вариация

Условие экстремума функционала:

Какое бы приращение аргумента мы ни взяли

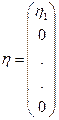Частный случай тоже

Исчезнет вся сумма и останется

Выбраны y 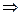зависит только от х.

Продифференцируем по частям

Воспользуемся основной леммой вариационного исчисления.

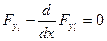
2)

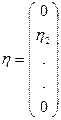
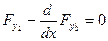
n)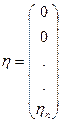

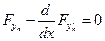
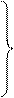
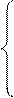
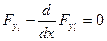
......................... cистема из n уравнений Эйлера

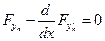
В каждое уравнение входят абсолютно все аргументы y₁,...,y_n (так как F(y₁,...,y_n))

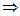решаем систему совместно

Пример 1:

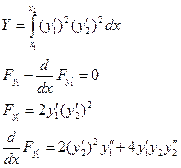
Пример 2:

Не зависит от y₂

Замечание:

Что, если есть еще и старшие производные переменного аргумента

С помощью переобозначений приведем к функциональной зависимости от первой производной.

Но можно записать уравнение Эйлера-Пуассона для каждой выбранной функции.

Вариационные задачи с подвижными границами

Найти кривую, которая имеет min расстояние

между окружностями

Разные точки влияют на

константу интегрирования

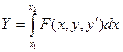
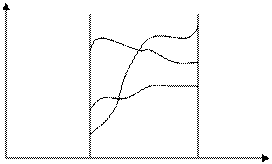y

y₂

y₁

x₁ x₂ x

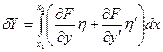- вариация функционала

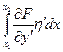- интегрируем по частям

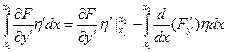
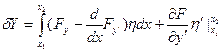
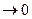
Кривая, удовлетворяющая уравнению Эйлера – экстремальная.

Найдено решение задачи (на графике), значит мы знаем y₁, y₂ 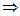мы можем найти кривую из уравнения Эйлера. В задачах с подвижными границами экстремальные оценки могут быть достигнуты только на экстремалях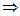

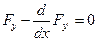из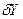

а это уравнение Эйлера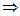

Там, где экстремаль есть

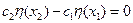
Если линейная комбинация при 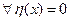, то с₂=0 или с₁=0

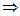дополнительные условия

В точке вхождения за границу и выхождения за границу

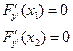
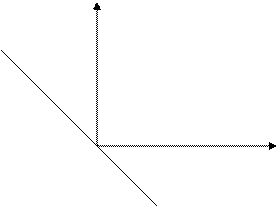
Надо найти прямую, имеющую min длину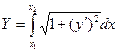

y = kx + b

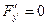при (то есть все у являются экстремалями)

отсюда следует что k = 0

В любом случае мы его не контролируем 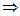оптимальные линии должны идти горизонтально, так как k = 0

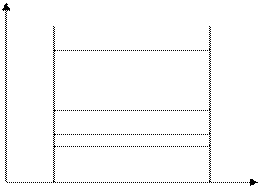y

x₁ x₂ x

Оценивая 2 точки, уравнение Эйлера ищет кратчайшее расстояние между ними

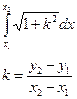
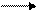
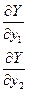0

Очевидно, что min функционала при y₂ – y₁=0

Ответ тот же самый, но это не метод вариацинного исчисления.

Общий случай:

Когда задана граница, по которой движется траектория

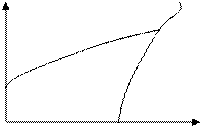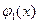
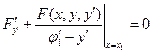
Условие вхождения в экстремальную границу – экстремаль должна войти под углом

Условия трансверсальности.

Другой тип задач:

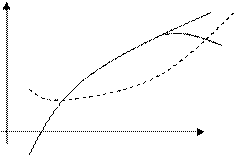Запретная область

Оптимальная кривая заходит в запретную область! Не подходит.

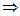оптимальная траектория идет по границе

Куски, которые не связаны с запретной областью, должны быть min (то есть экстремальны)
В задачах с запретными областями экстремаль касается запретной области.

Лекция №9

Метод неопределенных множителей Лагранжа в задачах вариационного исчисления.

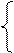
y = f(x₁,x₂)

y(x₁,x₂) = 0 – ограничение

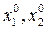
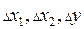имеет один знак (не имеет дифференциала)

Главное условие экстремума

Приращение можно заменить дифференциалом dy имеет один знак независимо от

dy = 0

В вариационном исчислении – вариация функционала

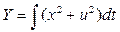
Если мы не можем исключить какой-либо аргумент – мы в тупике

с₁dx₁ + c₂dx₂ = 0 при c₁, c₂ = 0 одновременно

Если c₁, c₂ 0, значит есть связь между дифференциалами.

Дифференциалы могут быть связаны:

x₁ + x₂ =1

dx₁ + dx₂ = 0

dx₁ = -dx₂

с₁dx₁ + c₂dx₂ =0

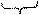c₁(dx₁-dx₁) = 0

=0

Если между аргументами есть связь, то и вариации связаны между собой

y = f(x₁,...,x_n)

y₁(x₁,...,x_n) = 0

...............

y_k(x₁,...,x_n) = 0

Даже если есть связь между аргументами, экстремум не меняется.

dy = 0

dx₂

dx₂ = -dx₁

dx₁

в точке экстремума (2)

Т.к. дифференциалы зависят, то коэффициенты нельзя приравнять к нулю.

(1) в любой точке

j = 1,...,k

n переменных и k уравнений определяют связь дифференциалов.

c₁₁dx₁ +................. + c_1ndx_n = 0

c_k1dx₁ +................. + c_kndx_n = 0

c₁₁dx₁ + c₁₂dx₂ +... + c_1kdx_k = - c_1k+1dx_k+1 – c_1ndx_n

c_k1dx₁ + c_k2dx₂ +... + c_kkdx_k = - c_kk+1dx_k+1 - c_kndx_n

свободные переменные

Теперь знаем связь между дифференциалами.

Коэффициенты при свободных дифференциалах обнулить.

Другой способ:

Каждое из соотношений (1) умножим на 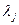и сложим с (2) – это для точек оптимума, так как (2) – соотношение только для точек оптимума.

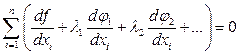
Делим дифференциалы на свободные и несвободные. При несвободных дифференциалах подбираются такие 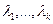, чтобы коэффициенты при них обнулились.

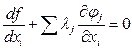
для свободных дифференциалов

Это можно записать и для свободных.

Для общего 0 коэффициенты при свободных тоже должны быть = 0.

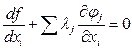i = 1,...,n для всех

n уравнений

Неизвестные:

x₁,...,x_n

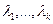(n+k) неизвестных

И еще +k уравнений-ограничений

В результате получается (n+k) уравнений и (n+k) неизвестных.

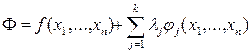
- наши n уравнений

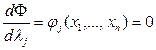- наши k ограничений

В вариационном исчислении все то же самое.

Постановка задачи:

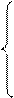
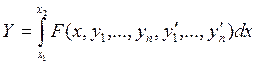
j = 1,...,k

Голономная (геометрическая) связь.

y₁(x) + y₂(x) = 0

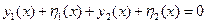
Вариации аргумента связанные.

Вариации бывают:

- зависимые

- независимые

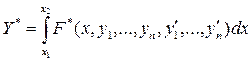
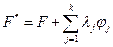
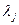зависит от х.

То же самое дифференциал ~ вариация

F^* содержит (n+k) аргументов.

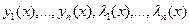
Имеется безусловный экстремум Y^* и найденные y₁(x),...,y_n(x) – есть экстремали. Для каждой функции напишем уравнение Эйлера.

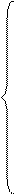
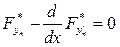
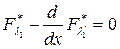
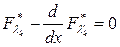
Система дифференциальных уравнений. Уравнения между собой связаны, то есть неавтономные.

(n+k) уравнений

Общий порядок должен быть 2*(n+k)

Пример

Задание условий закрепления

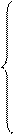
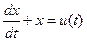
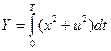
х(0) = х₀ 2 функции

х(Т) = х_Т

Оказывается, не все уравнения Эйлера – 2-го порядка

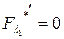
Уравнение Эйлера: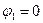

Пример:

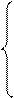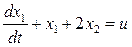
Общий порядок – первый.

x₁ + x₂ = 0

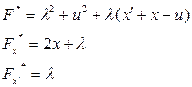
Уравнение Эйлера: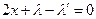

Порядок закрепления – 2. Два начальных условия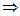

сможем определить наши неизвестные

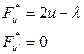
Уравнение Эйлера: 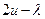= 0

Уравнение Эйлера: 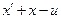= 0

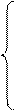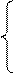
Продифференцируем по t второе уравнение.

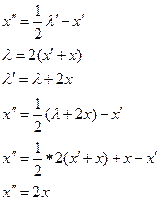
Найдем х, подставим в исходное и найдем u.

Мы вводим функционал, чтобы учесть ограниченность u.

Лекция №10

Дата добавления: 2015-06-27