Принцип максимума Понтрягина

Достаточные условия экстремума функционала

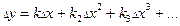
- аналогичный ряд Тейлора.

(вторая вариация – вариация от первой вариации)

квадратичный функционал.

Линейный функционал – функционал, зависящий от 2 аргументов. Если фиксируется один аргумент, то по второму аргументу функционал является линейным.

Пример1:

Квадратичный функционал – билинейный функционал, у которого f₁(x) = f₂(x).

Пример 2:

Пример 3:

y(x)= 0 – точка, подозрительная на экстремум (и на системность)

вариация от первой вариации

y(x) = 0

Пример:

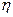
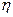(x) = x

нет экстремума

x

Обычно из условия задачи следует, существует ли 2-й экстремум.

Почему нам не хватает вариационного исчисления? Мы ищем экстремумы, а не min и max значения.

Пример:

- наибольшее значение

Экстремумы

При получения принципа максимума используется линеаризация дифференциальных уравнений.

Линеаризация дифференциальных уравнений:

Пусть известно решение x(t) при выбранном u(t)

Каково , если

Предполагаем, что изменение таково, что мало, если мало (то есть решение устойчивое)

- малы

а(t) b(t) c(t)

- это дифференциальное уравнение относительно при известном

Находим и

Обычно x(t) = const, u(t) = const 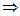a(t), b(t), c(t) = const

Тогда получаем дифференциальное уравнение с постоянными коэффициентами.

Это и есть метод линеаризации.

Важнейшее понятие в принципе максимума Понтрягина – понятие системы.

Важное понятие – переменные состояния, описывают систему в форме Коши.

x₁(t),....,x_n(t) – переменные состояния

Задача принципа максимума – надо перевести эту систему в другую так, чтобы функционал принял наибольшее/наименьшее значение.

Лекция №11

i = 1,2,..,,n

x(0) = x₀

x(T) = x_T

|u(t)| u_Н – область допустимых значений должна быть замкнутой

Y =

u

a b – в открытой точке

y_M

.

Игольчатая вариация

U

u_M

r

u(t)

t₀ t

-u_M

Импульс r должен иметь площадь отличную от 0.

- изменилось, т.к в точке начинает воздействовать

другое управляющее

воздействие

х(t) – cоотв. u(t)

игольчатая вариация

r

r-

Вводится дополнительная переменная

x₀(t) =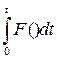

x₀(0) = 0

x₀(T) = Y

Если даем управляющее воздействие, то x₀ меняется в одну сторону.

Начинаем занимать линеаризацией.

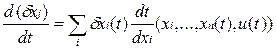
известно

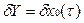
Пусть х*(t) – оптимальная траектория (u*(t))

скалярное произведение

U условие

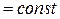
= 0

- сопряженные уравнения

Введем функцию Н:

Найдем

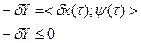
и другие u(t), x(t)

Теорема произвольности

Для того, чтобы u(t) – opt, необходимо, чтобы в момент t функционал Н достигал наибольшего значения по аргументу u

За пределы [-u_max;u_max] u выйти не может.

Это и есть принцип max правдоподобия.

Для систем, требующих min 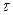, принцип максимума упрощается.

Лекция №12

Дата добавления: 2015-06-27