Поиск глобального экстремума функции в заданной области методом Монте – Карло

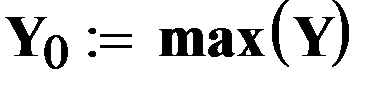Нелинейные функции в большинстве случаев имеют не один, а несколько экстремумов. Самый большой максимум или минимум называется глобальным экстремумом, остальные – локальными. При решении задачи, как правило, необходимо определение глобального экстремума. Ниже дается решение такой задачи в Маткаде для заранее заданной области. Вне нее глобальный экстремум может быть другим.

Пусть задана многоэкстремальная функция

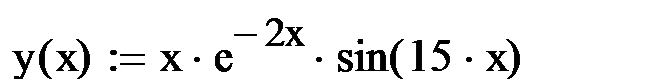
Рассмотрим ее графики при различных пределах изменения аргумента x:

Из рис.1 видно, что для области изменения аргумента -2<=x<=4 видно, что глобальный экстремум находится в районе x=-2 и равен примерно 75.

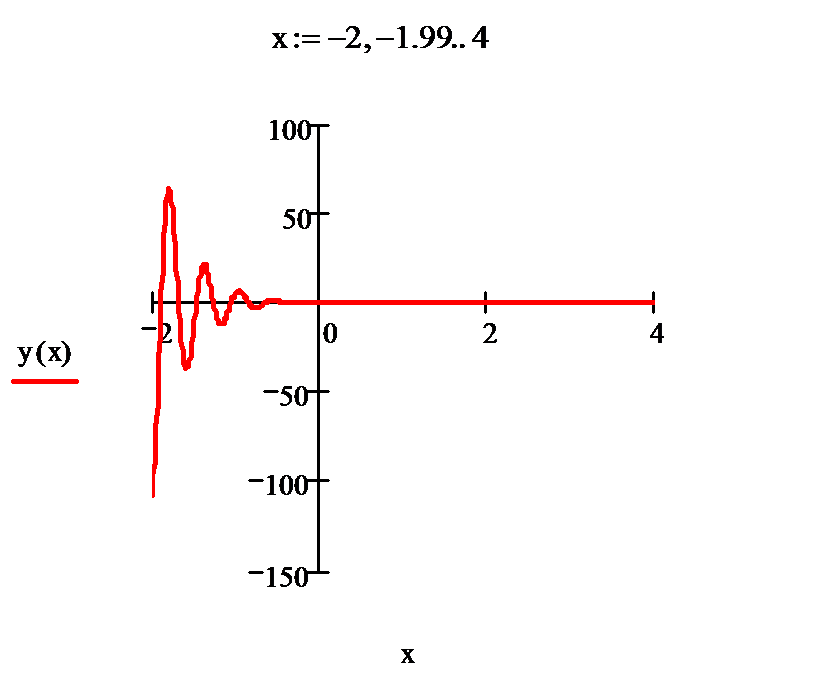
Рис.1

Из рис.2 следует, что для другой области изменения аргумента глобальный экстремум находится районе x=0.5

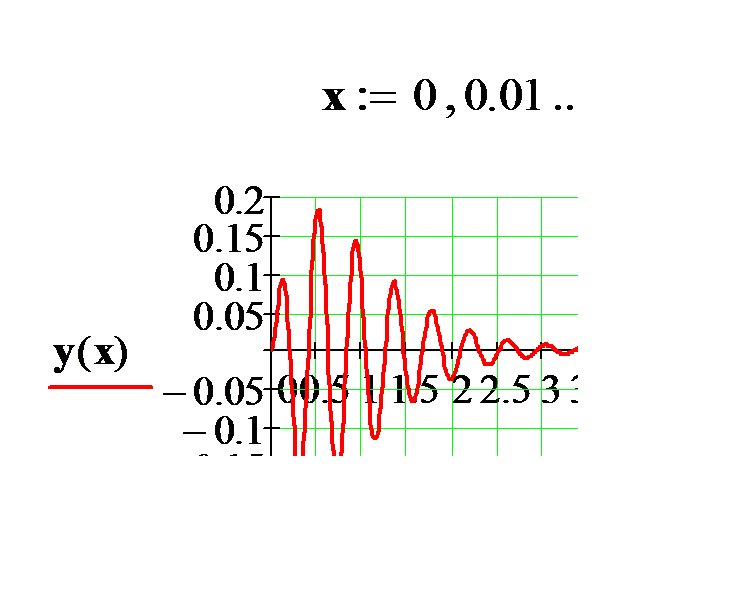
Рис.2

Найдем глобальный минимум этой функции в пределах изменения аргумента 0<x<3, используя метод Монте-Карло. Сформируем два вектора X и Y, присвоив их нулевым элементам значение нуль.

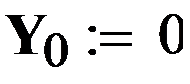
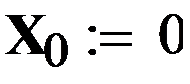
Зададимся количеством случайных чисел N, которые мы будем использовать для вычисления минимума. Чем больше это количество, тем точнее будет

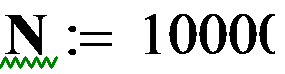
С помощью функции rnd(x) создадим вектор случайных значений элементов х _i . Функция rnd(x) генерирует равномерно распределенные случайные числа в интервале 0-х. Из графика видно, что нам достаточен интервал 0-3.

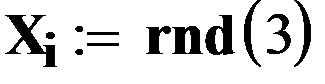
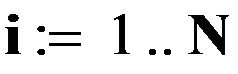
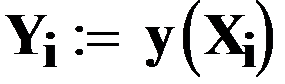Теперь в векторе Х помещено 100000 случайных чисел. Вычислим значения функции от них и поместим их в вектор Y.

Величину максимального элемента этого вектора найдем, используя функцию max.

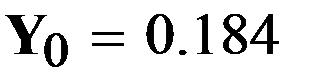
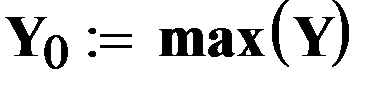
Мы вычислили (приближенно) максимальное значение заданной функции. Теперь необходимо определить значение аргумента, соответствующее минимальному значению функции..Для этого составим небольшую программку и вычислим по ней ответ:

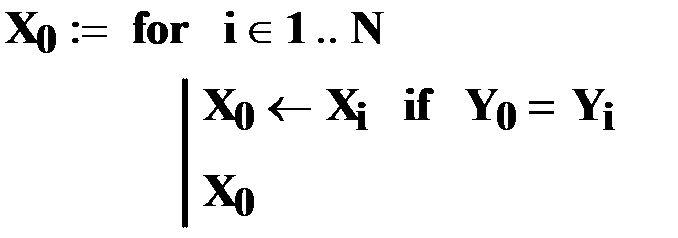
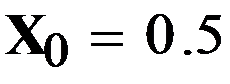
Задача 4. Вычислить максимумы и минимумы нижеприведенных функций:

ЛАБОРАТОРНАЯ РАБОТА № 3. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВА-

Дата добавления: 2015-06-27