Квантовая жидкость. Спектр бозевского типа

Термодинамическая величина в общем случае для жидкостей вычислить не удается (в отличие от газов или кристаллов). Причина – сильное межмолекулярное взаимодействие, различное для разных жидкостей.

Однако, общее теоретическое рассмотрение, возможно для жидкостей вблизи абсолютного нуля. И хотя имеется всего одно вещество – гелий, которое остается жидким вплоть до абсолютного нуля, этот вопрос имеет принципиальный интерес. Почему?

Согласно классической механике все тела должны быть твердыми при абсолютном нуле. Гелий же, благодаря особой слабости межмолекулярного взаимодействия, остается жидким вплоть до температур, при которых становятся существенны квантовые эффекты (квантовая жидкость), после чего затвердевание уже вообще не должно наступать (нулевые колебания).

Вычисление термодинамических величин требует знания спектра уровней энергии данного тела (именно спектр уровней, соответствует стационарным состояниям всей жидкости, а не отдельных атомов).

При достаточно низких температурах в стат. сумме должны учитываться лишь слабо возбужденные уровни энергии жидкости, т.е. уровни, расположенные не слишком высоко над нормальным (основным, невозбужденным).

При этом, всякое слабо возбужденное состояние макроскопического тела может рассматриваться как совокупность отдельных элементарных возбуждений.

Эти элементарные возбуждения ведут себя как некоторые квазичастицы, обладающие определенными энергиями и импульсами. До тех пор, пока их число достаточно мало, они не взаимодействуют друг с другом, так что их совокупность можно рассматривать как некий идеальный газ.

Пример квазичастиц – фононы в твердом теле.

Один из возможных типов энергетического спектра слабо возбужденных состояний квантовой жидкости (спектр бозевского типа) характеризуется тем, что элементарные возбуждения могут появляться исчезать поодиночке. Но момент количества движения всякой квантовомеханической системы (всей жидкости) может испытывать изменения лишь на целое число.

Поэтому, возникающие поодиночке элементарные возбуждения, должны обладать целочисленным моментом и подчинятся статистике Бозе.

Важнейшей характеристикой квазичастиц является их закон дисперсии – зависимость энергии от импульса.

В рассматриваемом спектре элементарные возбуждения с малыми импульсами 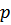(т.е. большими длинами волн 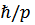) соответствуют обычным звуковым волнам в жидкости, т.е. представляют собой фононы. Это значит, что энергия таких элементарных возбуждений является линейной функцией импульса

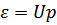
Где 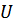– скорость звука, 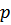– истинный импульс, а не квазиимпульс!

По мере увеличения импульса кривая 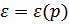отклоняется от линейной зависимости; дальнейший её ход зависит от конкретного вида межмолекулярного взаимодействия и не может быть вычислен в общем виде. Следует отметить, что при достаточно больших импульсах 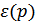вообще не может существовать, так как элементарные возбуждения со слишком большими импульсами неустойчивы и распадаются на несколько возбуждений с меньшими импульсами и энергиями.

Значение 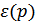при малых 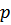позволяет вычислят термодинамические величины жидкости; при низких температурах все элементарные возбуждения обладают малыми энергиями, т.е. являются фононами. Поэтому можно применить прежние формулы для термодинамических величин. Разница заключается в том, что вместо возможных направлений поляризации в кристалле, в жидкости существует лишь одно продольное. Поэтому все выражения для термодинамических величин следует разделить на три.

Тогда

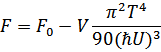
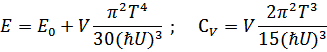
Энергетическим спектром рассматриваемого типа обладает жидкий гелий ()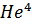

Анализ экспериментальных данных по термодинамическим величинам показывает, что 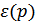может быть представлено следующим графиком

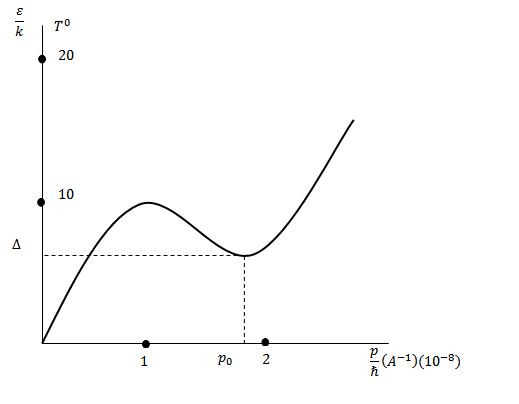
После начального линейного возрастания функция 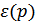достигает максимума, затем убывает, испытывая при 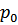минимальное значение.

При тепловом равновесии большинство элементарных возбуждений имеет энергии в области вблизи минимумов, т.е. вблизи 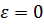и вблизи 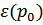. Поэтому именно эти области особенно существенна. Вблизи точки нуль имеем 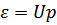. Вблизи точки 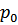функция 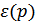может быть разложена в ряд по степеням разности :

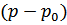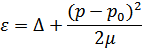
Где 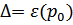и 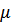– некоторые постоянные. Квазичастицы этого типа называют ротонами.

Эмпирические значения таковы:

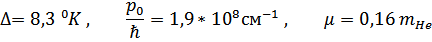
При 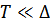(вблизи нуля это так) можно говорить о ротоном газе (их мало!). Поэтому вместо распределения Бозе можно использовать распределение Больцмана.

Поэтому для вычисления «ротонной» части свободной энергии применяем формулу

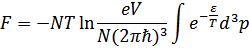
В свою очередь, число ротонов не является заданным, а само определяется условием минимума свободной энергии: ,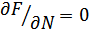

Что даст

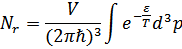
В результате

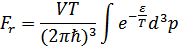
Подставим в эти формулы 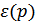, что даст

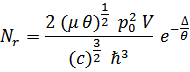
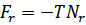
Отсюда находим вклад ротонов в энтропию и теплоемкость.

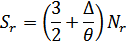
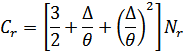
Таким образом, температурная зависимость ротонной части термодинамических величин в основном экспоненциальна. Поэтому при низких температурах (для жидкого 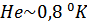) фотонная часть меньше фононной, а при более высоких температурах положение меняется и ротонный вклад превосходит фононный.

Дата добавления: 2014-01-03