Эффективная масса квазичастиц

Обозначим через энергии квазичистицы, вызванное отклонением ср.р. от «ступеньки»

где – вторая вариационная производная от 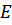и симметрична по 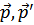. В приближении идеального газа .

Для простоты зависимость от спина не рассматриваем.

Вычислим импульс жидкости, отнесенный к единице объема. Скорость квазичастицы есть

Тогда поток квазичастиц дается интегралом

Поскольку число квазичастиц совпадает с числом истинных частиц, то для получения полного переноса массы квазичастиц, надо умножить поток их числа на массу «» истиной частицы. Таким образом

Варьируя обе стороны равенства по «» и используя определения , получим

(во втором интеграле мы заменили обозначение переменных и проинтегрировали по частям)

Ввиду произвольности , получим

Применим это соотношение к импульсам вблизи границы распределения Ферми. Тогда 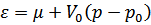, а производная

Это позволяет провести интегрирование по величине импульса

В функции 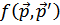оба аргумента взяты по абсолютной величине , так функция зависит только от угла между векторами .

Подставим это в определение .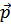

Умножим обе части на 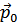и затем разделим на , что даст

Далее вычислим сжимаемость Ферми-жидкости и скорость звука в ней ()

Удобно выразить через производную от химпотенциала ()

Так как при 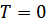имеем

Таким образом

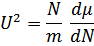
Поскольку , то вариация при изменении на

Второй член связан с тем, что предельный импульс нормирован на число частиц

и 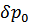связаны соотношением

Поскольку отлично от нуля лишь при , то можно записать в интеграле

Подставляя это в выражение для и определяя согласно

получим

Наконец, подставляя сюда и умножая на

получим окончательно

Описанный спектр при определенных условиях может оказаться неустойчивым и жидкость переходит в состояние с другим спектром (с энергетической «щелью»), в котором она обладает свойством сверхтекучести. Характер этого спектра можно рассмотреть на модели Ферми-газе со слабым притяжением между частицами.

ТЕМА № 7

Дата добавления: 2014-01-03