Вырожденный «почти идеальный» Ферми газ с притяжением между частицами

В случае притяжения между частицами, найденное выше выражение для основного состояния, оказывается недействительным, так как в системе происходит перестройка с понижением энергии.

Указание на источник перестройки дает анализ формулы для .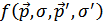

Функция 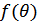имеет особую точку при 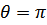, т.е. при противоположно направленных импульсах двух квазичастиц:

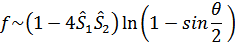
т.е. особенность существует лишь при антипараллельных спинах (при параллельных спинах 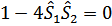и особенности нет).

Это означает, что тот вариант теории возмущений (для 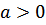) неприменим в случае взаимодействия пар частиц с противоположными спинами и импульсами.

Далее будет показано, что в случае притяжения именно это взаимодействие приведет к качественно новым явлениям.

Таким образом, приходим к выводу, что система операторов 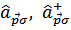, соответствующая свободным состояниям отдельных частиц газа, не может служить правильным исходным приближением теории возмущений.

Вместо них надо уже сразу ввести новые операторы, которые будем искать в виде линейных комбинаций

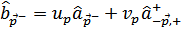
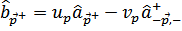
Объединяющих операторы частиц с противоположными импульсами и спинами.

Эти операторы должны удовлетворять таким же правилом коммутации Ферми, как и старые операторы

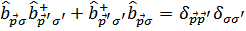
Все другие пары операторов антикоммутируют. Для этого коэффициенты преобразования должны удовлетворять условию .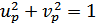

При этом обратные преобразования имеют вид

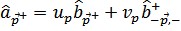
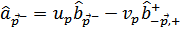
По тем же причинам, оставляем в гамильтониане члены, в которых

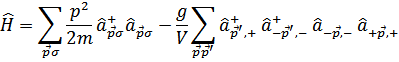
Где 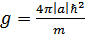(амплитуда рассеяния – отрицательная величина)

Эта форма записи уже предполагает основную роль взаимодействий с противоположными спинами и импульсами (дальше нет никакой теории возмущений)

Далее нужно будет диагонализовать гамильтониан.

Удобно, однако, предварительно отказываться от необходимости учитывать в явном виде постоянства числа частиц (фермиона). Для этого надо вместо функции Гамильтона ввести разность 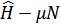, где число частиц 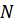само рассматривается как переменная величина. Химический потенциал затем и определяется условием равенства среднего 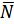заданному 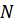числу частиц в системе.

В методе вторичного квантования это означает, что вместо 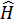вводится разности
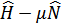, где оператор .

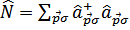Ниже мы будем обозначать через 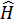именно эту разность.

Введем также обозначения

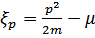– отклонение энергии от уровней Ферми

Поскольку 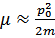, то вблизи поверхности Ферми

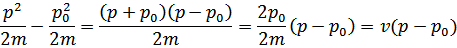
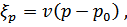
где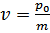

Таким образом (после вычитания 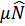) получим гамильтониан в следующем виде

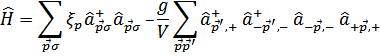
Теперь в гамильтониане произведем преобразование операторов. Совершая одновременную замену 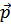на 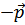, получим (суммируя по )

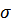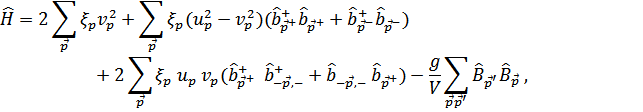
где мы обозначили

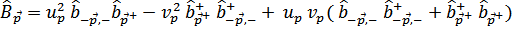
Выбор коэффициентов 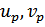определяется из условия минимума энергии 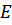системы при заданных числах заполнения .

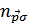В гамильтониане диагональные матричные элементы имеют лишь члены, содержащие произведения

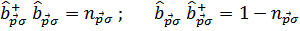
Поэтому сразу запишем выражение для энергии

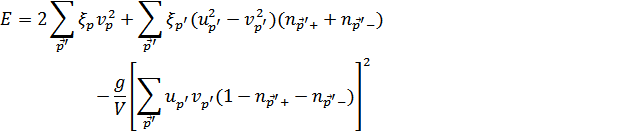
Варьируя это выражение по параметру 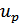(учитывая, что 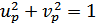), получим в качестве условия минимума

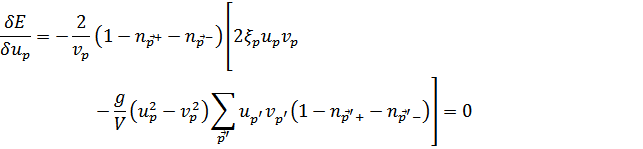
Отсюда находим уравнение (трансцендентное; решение есть не всегда)

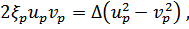
где введено обозначение

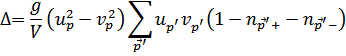
Используя определение 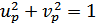получим

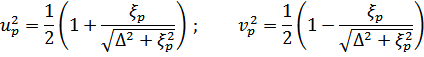
Подставляя эти выражения в определение 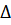, найдем, что

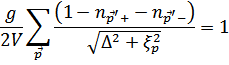
(уравнение, определяющее ).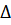

Исследуем полученное выражение. При 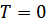квазичастица отсутствует: .

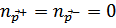Заметим сразу, что уравнение для 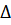заведомо не может иметь решения для 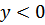(в случае отталкивательных потенциалов)

Переходя от суммирования к интегрированию, получим

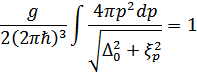
Основной вклад вносит область импульсов, в которой

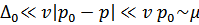
А интеграл имеет логарифмический характер. При этом

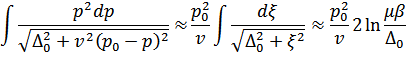
Где 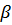– численный коэффициент.

Поэтому находим

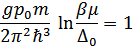
Откуда получаем

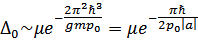
Поскольку 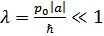(рассеяние медленных частиц), то 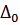экспоненциально мало по сравнению с .

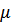Наибольший интерес представляет формула энергетического спектра системы, то есть энергия 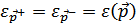элементарных возбуждений. Она находится вариацией 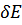по 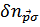(это можно делать при постоянстве )

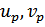Тогда имеем

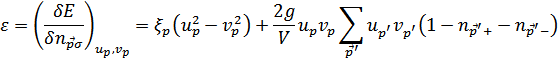
Подставляя сюда все необходимые величины, получим

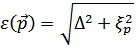
Отсюда видно замечательное свойство энергетического спектра рассматриваемой системы: энергия квазичастицы не может быть меньше величины 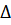, достигаемой при 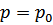. Другими словами, возбужденные состояния отделены от основного – энергетической щелью. Обладая полуцелым спином, квазичастица должна появляться парами. В этом смысле можно сказать, что величина щели равна .

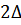Таким образом, спектр удовлетворяет установленному ранее условию: минимальное значение 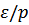отлично от нуля. Поэтому Ферми-газ с притяжением между частицами должен обладать свойством сверхтекучести.

ТЕМА №9

Приведены законы дисперсии в сверхтекучей (верхняя кривая) и нормальной Ферми-жидкости.

Величина щели 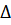зависит от температуры, т.е. сама форма спектра зависит от статистического распределения квазичастиц – ситуация аналогичная теории нормальной ферми-жидкости.

Поскольку при возрастании температуры 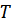числа заполнения квазичастиц возрастают, стремясь к 1 (к 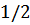), то 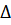при этом уменьшается и при некоторой конечной температуре 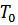обратится в ноль: система перейдет из сверхтекучего состояния в нормальное.

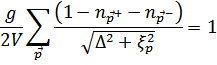
Эта точка представляет собой фазовый переход второго рода (подобный переходу в жидком гелии).

Наличие энергетической щели можно истолковать наглядно как результат образования связанных состояний парами притягивающихся частиц.

Тогда величина 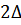есть энергия, которая необходима для разрыва такой пары. Этот эффект возникает в Ферми-газе уже при сколь угодно слабом притяжении. Обладая равным нулю спином, пара ведет себя, как бозевские образования, и могут накапливаться на уровне наименьшей энергии – уровне с равным нулю суммарным импульсом. В таком наглядном истолковании это явление вполне аналогично накапливанию частиц в состоянии с нулевой энергией в бозе-газе (бозе-эйнштенвская конденсация).

Однако, представление о связанных парах не следует принимать в буквальном смысле. Более строго можно говорить о корреляции между импульсами пары частиц, приводящей к конечной вероятности иметь равную нулю сумму импульсов.

Оценим радиус корреляции частиц с нулевым импульсом.

Разброс значений 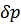пропорционален энергии 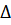, т.е. .

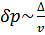Соответствующая длина 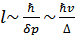определяет порядок величины расстояний между частицами с коррелированными импульсами.

Эти величины есть

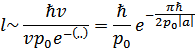
Поскольку совпадает с порядком величины межатомных расстояний, то 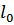велико по сравнению с ними. Это обстоятельство наглядно демонстрирует условность понятия о связанных парах.

Далее найдем температурную зависимость энергетической щели, т.е. .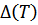

Перепишем уравнение для 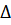в следующем виде

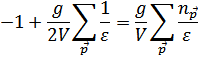
Здесь учтено, что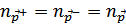

Но левая часть отличается от того, что было ранее, только заменой 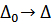. Поэтому, с учетом ранее полученных результатов, левая часть равна

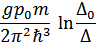
В правой части уравнения вместо 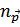подставляем её явное выражение и переходим от суммирования к интегрированию по

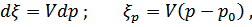
что даст

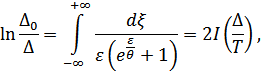
где мы обозначили

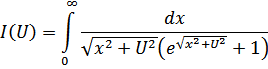
Ввиду быстрой сходимости интеграла пределы распространены на .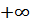

В области низких температур ()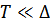

(первый член разложения по степеням )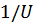

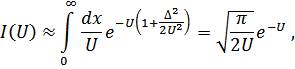
что даст следующее уравнение

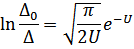
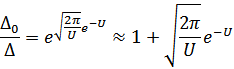
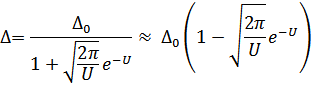
В области вблизи точки перехода 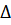мало и первые члены разложения интеграла 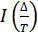дают

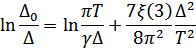
Отсюда видно, что 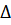обращается в ноль при температуре

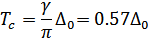
Малой по сравнению с температурой вырождения .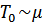

После этого в первом порядке по 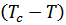получим

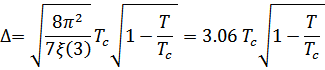
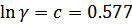– постоянная Эйлера

Вычислим теперь теплоемкость газа в области низких температур. Проще всего находить из формулы

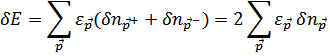
Для изменения полной энергии при варьировании чисел заполнения частиц. Разделив на 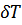и перейдя от суммирования к интегрированию, получим

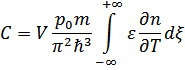
При 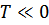функция распределения квазичастиц есть 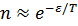, так что имеем

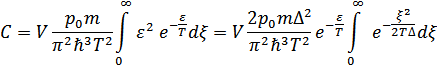
Или окончательно

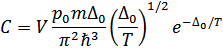
Таким образом, при 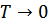теплоемкость убывает по экспоненциальному закону – прямое следствие наличия щели в энергетическом спектре.

ТЕМА №10

Дата добавления: 2014-01-03