
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сверхтекучесть
|
|
|
|
Квантовая жидкость со спектром вышеуказанного типа должна обладать свойством сверхтекучести.
Начнем рассмотрение при 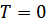 .
.
При этой температуре жидкость находится в своем нормальном, невозбужденном состоянии.
Пусть жидкость протекает по капилляру с постоянной скоростью 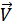 . Наличие вязкости приводило бы к тому, что постепенно жидкость замедлила скорость и, в конечном счете, прекратилось движение.
. Наличие вязкости приводило бы к тому, что постепенно жидкость замедлила скорость и, в конечном счете, прекратилось движение.
Нам будет удобно рассматривать течение в системе координат, движущейся вместе с жидкостью. В этой системе гелий покоится, а стенки капилляра движутся со скоростью (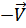 ). При наличии вязкости покоящийся гелий тоже должен бы начать двигаться. Физически очевидно, что увлечение жидкости стенками трубки не может привести с самого начала к движению жидкости как целого. Появление движения должно начаться с постепенного возбуждения внутренних движений, т.е. с появления в жидкости элементарных возбуждений.
). При наличии вязкости покоящийся гелий тоже должен бы начать двигаться. Физически очевидно, что увлечение жидкости стенками трубки не может привести с самого начала к движению жидкости как целого. Появление движения должно начаться с постепенного возбуждения внутренних движений, т.е. с появления в жидкости элементарных возбуждений.
Предположим, что в жидкости появляется одно элементарное возбуждение с импульсом 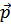 и энергией
и энергией 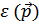 . Тогда энергия
. Тогда энергия 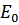 жидкости (в системе, где она первоначально покоилась) сделается равной энергии
жидкости (в системе, где она первоначально покоилась) сделается равной энергии 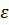 этого возбуждения, а её импульс
этого возбуждения, а её импульс 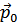 – импульсу
– импульсу 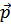 . Перейдем теперь обратно к системе координат, в которой покоится капилляр. Согласно формулам механики имеем
. Перейдем теперь обратно к системе координат, в которой покоится капилляр. Согласно формулам механики имеем
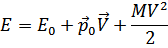
Где 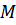 – масса жидкости. Подставляя
– масса жидкости. Подставляя 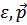 , вместо
, вместо 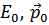 , получим
, получим
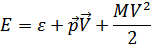
Член 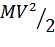 представляет собой первоначальную кинетическую энергию движущейся жидкости. Выражение (
представляет собой первоначальную кинетическую энергию движущейся жидкости. Выражение (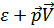 ) есть изменение энергии благодаря появлению возбуждения. Это изменение должно быть отрицательно, т.к. энергия движущейся жидкости должна уменьшаться
) есть изменение энергии благодаря появлению возбуждения. Это изменение должно быть отрицательно, т.к. энергия движущейся жидкости должна уменьшаться 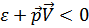
При заданном значении 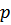 , левая часть имеет минимальное значение при антипараллельных
, левая часть имеет минимальное значение при антипараллельных 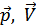 , поэтому должно быть
, поэтому должно быть 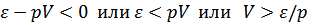 (это условие появления элементарных возбуждений)
(это условие появления элементарных возбуждений)
Тогда при 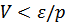 получаем, что элементарных возбуждений нет, т.е. наблюдаем сверхтекучесть.
получаем, что элементарных возбуждений нет, т.е. наблюдаем сверхтекучесть.
Таким образом, к сверхтекучести приведет всякий спектр, в котором достаточно малые возбуждения являются фононами.
Рассмотрим теперь ту же жидкость при 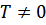 (вблизи нуля). В этом случае жидкость не находится в основном состоянии – она содержит возбуждения. Приведенные выше соображения остаются в силе (нигде не было непосредственно использовано обстоятельство, что жидкость находилась первоначально в основном состоянии). Движение жидкости со скоростью
(вблизи нуля). В этом случае жидкость не находится в основном состоянии – она содержит возбуждения. Приведенные выше соображения остаются в силе (нигде не было непосредственно использовано обстоятельство, что жидкость находилась первоначально в основном состоянии). Движение жидкости со скоростью 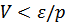 не может привести к появлению в ней новых элементарных возбуждений. Однако, что будет с уже существующими возбуждениями?
не может привести к появлению в ней новых элементарных возбуждений. Однако, что будет с уже существующими возбуждениями?
Для этого проведем следующие вычисления. Представим себе, что «газ квазичастиц» движется как целое относительно жидкости поступательно (сквозь жидкость) со скоростью 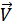 . Функция распределения для движущегося как целое газа, получается из функции распределения
. Функция распределения для движущегося как целое газа, получается из функции распределения 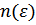 «неподвижного» газа путем замены энергии
«неподвижного» газа путем замены энергии 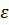 частицы величиной
частицы величиной 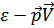 , где
, где 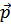 – импульс частицы. Поэтому полный импульс газа (отнесенный к единице объема) будет
– импульс частицы. Поэтому полный импульс газа (отнесенный к единице объема) будет
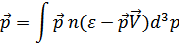
Предположим, что скорость 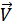 мала и разложим подынтегральное выражение по степеням
мала и разложим подынтегральное выражение по степеням 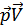 . Член нулевого порядка исчезает при интегрировании по направлениям вектора
. Член нулевого порядка исчезает при интегрировании по направлениям вектора 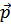 , и остается
, и остается
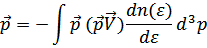
Проводя интегрирование по направлениям вектора 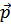 , получим
, получим
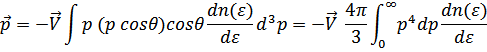
Для фононов 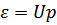 и выполняя интегрирование по частям, получим
и выполняя интегрирование по частям, получим
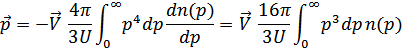
Учтем, что
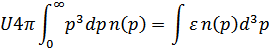
Представляет собой энергию 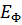 единицы объема фононного газа, так что
единицы объема фононного газа, так что
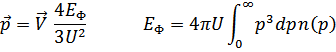
Прежде всего мы видим, что движение «газа квазичастиц» сопровождается переносом некоторой массы: эффективная масса единицы объема газа – коэффициент пропорциональности между импульсом 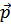 и скоростью
и скоростью 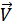 . С другой стороны, при течении жидкости по капилляру ничто не мешает «частицам» этого газа сталкиваться со стенками трубки и обмениваться с ними импульсом.
. С другой стороны, при течении жидкости по капилляру ничто не мешает «частицам» этого газа сталкиваться со стенками трубки и обмениваться с ними импульсом.
В результате «газ возбуждений» (существующий при 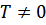 ) будет остановлен, как это произошло бы со всяким обычным газом, протекающим по капилляру.
) будет остановлен, как это произошло бы со всяким обычным газом, протекающим по капилляру.
Таким образом, приходим к выводу: при 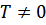 часть массы жидкости будет вести себя как всякая нормальная жидкость, «цепляющаяся» при движении о стенки сосуда; остальная часть массы будет вести себя как не обладающая вязкостью сверхтекучая жидкость. При этом, между этими движущимися друг через друга частями массы жидкости «нет трения», т.е. не происходит передачи импульса от одной из них к другой.
часть массы жидкости будет вести себя как всякая нормальная жидкость, «цепляющаяся» при движении о стенки сосуда; остальная часть массы будет вести себя как не обладающая вязкостью сверхтекучая жидкость. При этом, между этими движущимися друг через друга частями массы жидкости «нет трения», т.е. не происходит передачи импульса от одной из них к другой.
ТЕМА №5
В квантовой жидкости могут существовать одновременно два движения, каждое из которых связано со своей «эффективной массой» (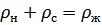 ).
).
Одно из этих движений «нормально», т.е. обладает теми же свойствами, что и движение обычной вязкой жидкости; другое – сверхтекучее. Оба эти движения происходят без передачи импульса от одного к другому. Особо подчеркнем, что здесь нет никакого разделения реальных частиц жидкости на нормальные и сверхтекучие.
Формулой
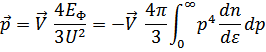
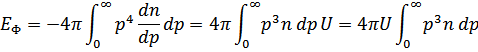
определяется нормальная часть массы жидкости при достаточно низких температурах (все элементарные возбуждения фонона) Тогда, учитывая, что
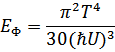
(было получено ранее для фононов в кристалле)
Найдем для нормальной части 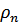 плотности жидкости:
плотности жидкости:
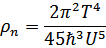
Это фононный вклад нормальной части плотности
Для вычисления ротонной части заметим
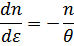
(следствие распределения Больцмана), что даст
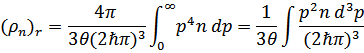
Поскольку 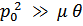 , то с достаточной степенью точности полагаем, что
, то с достаточной степенью точности полагаем, что 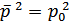 , таким образом
, таким образом
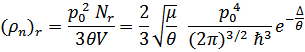
Ротонная часть 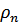 сравнивается с фононной при
сравнивается с фононной при 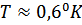 , а при больших температурах становится преобладающей.
, а при больших температурах становится преобладающей.
По мере повышения температуры всё большая часть массы жидкости становится нормальной. В точке, в которой нормальной становится вся масса, сверхтекучесть исчезает. Это так называемая 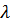 – точка фазового перехода 2 рода.
– точка фазового перехода 2 рода.
Участок кривой 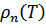 вблизи
вблизи 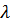 – точки не может быть вычислен точно. Но ввиду быстрого возрастания (экспоненциального)
– точки не может быть вычислен точно. Но ввиду быстрого возрастания (экспоненциального) 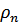 , можно ожидать, что температуру
, можно ожидать, что температуру 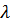 – точки можно получить используя последнюю формулу и полагая
– точки можно получить используя последнюю формулу и полагая 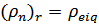 . Такое вычисление дает
. Такое вычисление дает 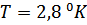 . Экспериментальное значение
. Экспериментальное значение 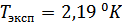 .
.
Фазовый переход второго рода всегда связан с появлением или исчезновением какого-либо качественного свойства. Для жидкого гелия с макроскопической точки зрения – это образование сверхтекучей компоненты. С микроскопической точки зрения речь идет об определенных свойствах матрицы плотности. Рассмотрим каких. Эта матрица определяется как интеграл
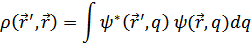
Здесь 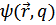 волновая функция тела;
волновая функция тела; 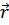 – радиус-вектор одной частицы;
– радиус-вектор одной частицы; 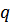 – совокупность координат всех остальных частиц, по координатам которых проводится усреднение.
– совокупность координат всех остальных частиц, по координатам которых проводится усреднение.
Для изотропного тела (жидкость)
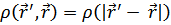
Для обычных жидкостей
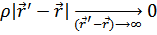
Для сверхтекучей жидкости
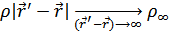
Рассмотрим к чему это приведет.
Вычислим Фурье – компоненты 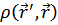
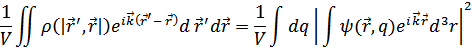
Это выражение задает распределение вероятностей различных значений импульса 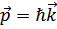 частицы.
частицы.
Для обычной жидкости 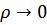 при
при 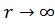 (интеграл сходится) вероятность при
(интеграл сходится) вероятность при 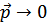 остается конечной (с нулевым импульсом очень мало частиц)
остается конечной (с нулевым импульсом очень мало частиц)
Для сверхтекучей жидкости 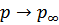 , при
, при 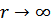 и при
и при 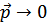 интеграл равен
интеграл равен 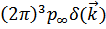 . Это означает, что конечное число частиц обладает нулевым импульсом.
. Это означает, что конечное число частиц обладает нулевым импульсом.
Таким образом, данное свойство матрицы плотности означает, что в сверхтекучей жидкости число частиц обладает нулевым импульсом (совокупность этих частиц нельзя отождествить со сверхтекучей частью жидкости)
В частности, при 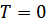 вся жидкость сверхтекуча, но не все частицы имеют нулевой импульс.
вся жидкость сверхтекуча, но не все частицы имеют нулевой импульс.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 734; Нарушение авторских прав?; Мы поможем в написании вашей работы!