Введение. Особенно часто процедура проверки статистических гипотез проводится для оценки существенности расхождений сводных характеристик отдельных совокупностей

Особенно часто процедура проверки статистических гипотез проводится для оценки существенности расхождений сводных характеристик отдельных совокупностей (групп): средних, относительных величин. Такого рода задачи, как правило, возникают в социальной статистике. Трудоемкость статистико-социологических исследований приводит к тому, что почти все они строятся на несплошном учете. Поэтому проблема доказательности выводов в социальной статистике стоит особенно остро. Применяя процедуру проверки статистических гипотез, следует помнить, что она может гарантировать результаты с определенной вероятностью лишь по «беспристрастным» выборкам, на основе объективных данных

Теоретико-вероятностные и статистические методы применяются в физике, техники, геологии, биологии, лингвистике, медицине, социологии, управлении и т. д., - всюду, где можно организовать эксперимент в виде случайной бесповторной выборки, в которой отдельные наблюдения независимы. Один из основных разделов статистики - теория проверки статистических гипотез. В процессе статистического анализа формулируют и проверяют предположения (гипотезы) относительно величины независимых параметров или закона распределения изучаемой генеральной совокупности. Так на стадии предварительного эксперимента происходит оценивание параметров и проверка статистических гипотез о воспроизводимости результатов эксперимента, о виде распределения результатов эксперимента, о наличии корреляционных связей между факторами и переменной состояния и др.

Ввиду огромного разнообразия видов статистических гипотез в предлагаемой методической разработке рассматриваются не все их виды, однако подробно рассмотрена общая схема проверки гипотез, приведены примеры решения задач и задания для самостоятельной работы.

Понятие статистической гипотезы. Общая схема проверки статистических гипотез

Под статистической гипотезой понимается всякое предположения о виде функции распределения или о ее параметрах.

Иными словами, статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Обозначается гипотеза буквой 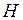. Так, может быть выдвинута гипотеза о том, что средняя в генеральной совокупности равна некоторой величине, о том, что «выборка извлечена из нормальной генеральной совокупности» или что «генеральные средние двух анализируемых совокупностей равны».

Гипотезы бывают:

- простые и сложные;

- параметрические и непараметрические;

- основные (выдвинутые) и альтернативные (конкурирующие).

Если выдвигаемая гипотеза сводится к утверждению о том, что значение некоторого неизвестного параметра генеральной совокупности в точности равно заданной величине, то эта гипотеза называется простой.

Например: «Дисперсия ошибки измерения равна 0,1»; «Среднее значение измеряемой величины равно 50,25».

Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез, при этом указывается некоторая область вероятных значений параметра.

Например: «Вероятность брака в партии больше 0,05».

Гипотезы о параметрах генеральной совокупности называются параметрическими, о распределениях - непараметрическими.

По своему содержанию статистические гипотезы можно подразделить на несколько основных типов:

- гипотезы о виде закона распределения исследуемой случайной величины;

- гипотезы о числовых значениях параметров исследуемой генеральной совокупности;

- гипотезы об однородности двух или нескольких выборок или некоторых характеристик анализируемых совокупностей;

- гипотезы об общем виде модели, описывающей статистическую зависимость между признаками; и др.

Выдвинутая гипотеза называется нулевой (основной). Ее обозначают 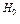и обычно формулируют в виде равенства.

По отношению к высказанной (основной) гипотезе всегда можно сформулировать альтернативную (конкурирующую), противоречащую ей. Альтернативную (конкурирующую) гипотезу принято обозначать .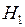

Нулевая гипотеза отвергается тогда, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен, в этом случае справедливой считают альтернативную гипотезу.

Вид альтернативной гипотезы определяется смыслом задачи.

Пример 1. В среднем, мешок сахара должен весить 50 кг. Кладовщиком фирмы принимается машина с мешками сахара. Выборочно перевешиваются несколько мешков, и если средний вес мешка 50 кг, то партия принимается, если меньше – возвращается поставщику как некондиционная. Таким образом, в этой ситуации требуется проверить гипотезу

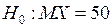при альтернативной гипотезе

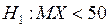
Пример 2. Исследуется содержание нитратов в партии овощей. Допустимая норма 0,01. Выборочно делается несколько замеров и если среднее значение содержания нитратов равно 0,01, то партия идет в продажу, если больше – бракуем. Т.е. проверяется гипотеза

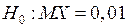при альтернативной гипотезе

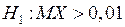
Пример 3. Cодержание активного ядохимиката в средстве для борьбы с садовыми вредителями должно составлять 0,001. Выборочно делается несколько замеров из разных пачек средства в партии. Если среднее значение содержания ядохимиката равно 0,001, то партия идет в продажу, если больше, то происходит отравление, если меньше – препарат не действует, – в обоих случаях партия бракуется. Т.е. проверяется гипотеза

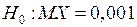при альтернативной гипотезе

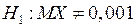
Общая схема проверки статистических гипотез

Чтобы с помощью различных критериев ответить на вопросы, поставленные перед исследователем, приходится проверять нулевую гипотезу об отсутствии эффекта, сравнивая при этом выборочные средние, доли, дисперсии и т.д.

Проверка любой статистической гипотезы осуществляется на основе выявления согласованности эмпирических данных с предполагаемыми (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных.

Для того чтобы считать H₀ доказанной нужно или вновь повторить эксперимент или проверить гипотезу с помощью других критериев.

Проверка статистических гипотез складывается из следующих этапов:

· выдвижение (формулировка) основной и альтернативной гипотез 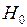и ;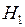

· выбор критерия проверки гипотезы (обозначим его в общем виде D);

· выбор уровня значимости α и определение критической точки k;

· вычисление значения критерия D, сравнение его с критической точкой и вынесение решения.

Рекомендации по выбору критерия D содержатся в специальной литературе по данной теме. Для проверки каждой статистической гипотезы разработаны критерии ее проверки, возможно даже несколько. Статистический критерий – это правило (формула), по которому определяется мера расхождения результатов выборочного наблюдения (действительной ситуации) с высказанной гипотезой .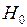

Например, мы думаем, что измеряемый нами признак имеет какой-то определенный вид распределения (скажем, показательное) и хотим убедиться в правильности своего предположения. Другими словами, нам нужно проверить гипотезу о виде распределения. Основная гипотеза

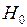: признак имеет показательное распределение

при альтернативной гипотезе

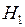: признак распределен не по показательному закону

Для проверки гипотезы всю область экспериментальных данных делят на интервалы 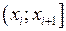. В качестве критерия часто используется критерий «хи-квадрат»:

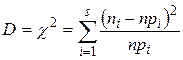, где

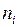- число экспериментальных точек, попавших в интервал ,

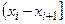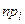- сколько точек должно было бы попасть в интервал 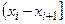, при показательном законе распределения экспериментальных данных.

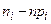- различие между действительным положением вещей и нашим предположением.

Если мы сделали правильное предположение, т.е. если распределение действительно показательное, то величины 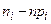будут малы и величина всего критерия D будет небольшая. Если же распределение не показательное, то различие между числом точек действительно попавших в каждый интервал 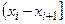и количеством точек, которые попали бы в этот интервал при показательном законе распределения данных будет сильно различаться, т.е. величины 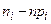будут большие и их сумма (т.е. значение всего критерия) тоже будет большой. Итак, если величина D, вычисленная по выборке, мала, то верна гипотеза 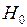, если велика – верна гипотеза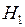

Остается понять, когда считать величину D большой. Т.е. нужна некоторая отметка на числовой оси, так называемая критическая точка. Если величина критерия D становится больше этой критической точки, считается, что различия между утверждением гипотезы 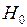и реальностью велики, и рассматриваемая гипотеза не согласуется с реальностью, т.е. считаем верной гипотезу 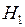. Если же критерий D оказывается меньше критической точки, считается, что различия между утверждением гипотезы 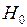и реальностью незначительны и обусловлены действием случайных факторов, т.е. считаем верной гипотезу 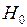. Для того чтобы считать H₀ доказанной нужно или вновь повторить эксперимент или проверить гипотезу с помощью других критериев.

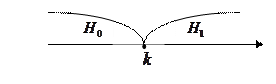
Как определить критическую точку? Зададим некоторую вероятность 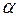попадания критерия D в критическую область. Тогда если 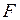- функция распределения критерия D, то

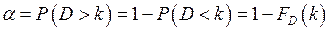
Критическая точка ищется путем решения уравнения 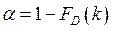, т.е. по таблице значений функции 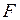(см. раздел «Построение критических областей»).

Из каких соображений выбирать значения 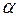? Этот вопрос связан с проблемой возникновения ошибок при проверке гипотез.

Дата добавления: 2015-07-13