Интегрирование рациональных дробей

Рациональной дробью называется отношение двух многочленов

.

Рациональная дробь называется правильной, если степень многочлена ниже степени многочлена ; в противном случае дробь называется неправильной.

Если дробь неправильная, то следует выделить целую часть, т.е. представить ее в виде суммы многочлена и правильной дроби.

Простейшими дробями называют правильные дроби четырех видов:

В случаях III и IV квадратный трехчлен не имеет действительных корней.

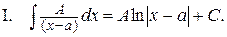
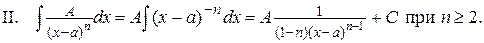
Интегрированию дробей III типа посвящен предыдущий пункт.

Любую правильную дробь можно разложить на сумму простейших дробей. Для этого знаменатель раскладывают на линейные и квадратичные множители так, чтобы квадратичные не имели вещественных корней.

Рассмотрим три важных случая.

1. раскладывается на линейные различные множители. Дробь представима в виде суммы n простейших дробей 1 типа.

2. Каждому линейному множителю кратности k, соответствует (k- 1) дробей 2 типа и одна дробь 1 типа

3. Каждому квадратичному множителю соответствует дробь III типа

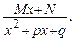
Коэффициенты находятся из условия, что равенства являются тождественными.

Случай, когда знаменатель содержит квадратичные кратные множители, мы не рассматриваем.

Пример 1. Найти интеграл

Решение. Под знаком интеграла неправильная дробь. Выделим целую часть, разделив числитель дроби на знаменатель:

Следовательно,

–

Пример 2. Найти интеграл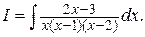

Решение. Подынтегральная функция – правильная дробь. Представим ее в виде суммы простейших дробей

(1)

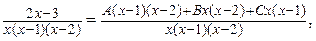
Найдем коэффициенты разложения методом частных значений. Полагая в полученном тождестве вместо значения: 0, 1, 2, получим

Подставив в равенство (1) найденные значения коэффициентов, имеем:

Пример 3. Найти интеграл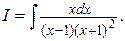

Решение.

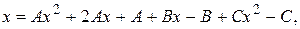
Приравнивая коэффициенты при получаем:

Пример 4. Найти интеграл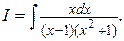

Решение. .

Приводя правую часть к общему знаменателю и приравнивая числители, получим: .

Комбинируя методы частных значений и сравнивая коэффициенты, найдем:

.

Дата добавления: 2017-01-13