
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные уравнения второго порядка
1. Основные понятия.
Линейными дифференциальными уравнениями второго порядка называются уравнения вида
 (I)
(I)
функции  ,
,  ,
,  непрерывны в некотором промежутке
непрерывны в некотором промежутке  .
.
Уравнение (I) называется линейным неоднородным или уравнением с правой частью, если  . Если
. Если  , то уравнение называется линейным однородным.
, то уравнение называется линейным однородным.
Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.
Теорема 1. Общее решение линейного неоднородного уравнения 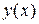 складывается из общего решения
складывается из общего решения  соответствующего ему однородного уравнения и частного решения
соответствующего ему однородного уравнения и частного решения  неоднородного:
неоднородного:

Ограничимся рассмотрением линейных уравнений с постоянными коэффициентами, которые широко используются в механике, электротехнике.
2. Линейное однородное уравнение с постоянными коэффициентами имеет вид:  , (II)
, (II)
где  – вещественные числа.
– вещественные числа.
Характеристическим уравнением называется уравнение  , его корни
, его корни  и
и  . Характеристическое уравнение получают заменой
. Характеристическое уравнение получают заменой  в данном линейном однородном уравнении.
в данном линейном однородном уравнении.
Теорема 2. 1) Если корни характеристического уравнения вещественные различные 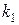 и
и  , то общее решение однородного уравнения
, то общее решение однородного уравнения
 , (II.I)
, (II.I)
2) если  =
=  =
=  , то
, то
 , (II.II)
, (II.II)
3) если корни комлексно-сопряженные 
 то
то
 (II.III)
(II.III)
Пример 1. Найти общее решение  .
.
Решение. Составим характеристическое уравнение  ;
;  ;
;  , по (II.I) имеем
, по (II.I) имеем  .
.
Пример 2. Найти частное решение уравнения  , если
, если  ;
;  .
.
Решение. 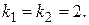 По (II.II) общее решение
По (II.II) общее решение 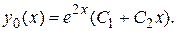 Выбираем
Выбираем  и
и 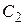 так, чтобы выполнялись начальные условия:
так, чтобы выполнялись начальные условия:  ;
;  ;
;  ;
;  ;
;  . Подставив найденные
. Подставив найденные  и
и 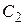 в общее решение, получим искомое частное решение:
в общее решение, получим искомое частное решение:  .
.
Пример 3. Найти общее решение  .
.
Решение. 
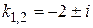 ;
; 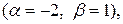 по (II.III) имеем общее решение:
по (II.III) имеем общее решение: 
Пример 4. Найти общее решение уравнения гармонических колебаний  .
.
Решение. 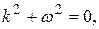

 по (II.III) общее решение
по (II.III) общее решение 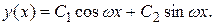
3. Линейные неоднородные уравнения с постоянными коэффициентами 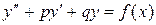 . Подбор частного решения методом неопределенных коэффициентов
. Подбор частного решения методом неопределенных коэффициентов
Этот метод, наиболее важный для приложений, применим только в том случае, когда правая часть уравнения имеет вид квазиполинома:

где 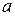 и
и  – действительные числа,
– действительные числа,  и
и  – многочлены степеней
– многочлены степеней  и
и  .
.
Теорема 3. Частное решение линейного неоднородного дифференциального уравнения следует искать в виде
1) если 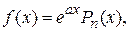 то (II.IV)
то (II.IV)
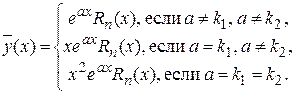
где 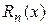 – многочлены с неопределенными коэффициентами степени
– многочлены с неопределенными коэффициентами степени  , записываются так:
, записываются так:  и т.д. Чтобы найти неопределенные коэффициенты, нужно частное решение
и т.д. Чтобы найти неопределенные коэффициенты, нужно частное решение  подставить в заданное уравнение.
подставить в заданное уравнение.
2) если  то (II.V)
то (II.V)
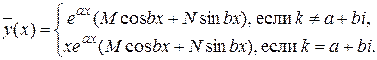
Коэффициенты  и
и  находят аналогично коэффициентам
находят аналогично коэффициентам 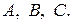 Если в функцию
Если в функцию  входит только
входит только 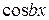 или
или  , в частное решение надо включать оба слагаемых.
, в частное решение надо включать оба слагаемых.
На основании теоремы 1 общее решение 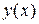 неоднородного уравнения складывается из общего решения однородного
неоднородного уравнения складывается из общего решения однородного  (теорема 2) и частного неоднородного
(теорема 2) и частного неоднородного  (теорема 3).
(теорема 3).
Пример 1. Найти общее решение дифференциального уравнения
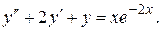
Решение. Общее решение данного уравнения имеет вид  где
где  – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения 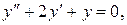 а
а  – частное решение данного неоднородного уравнения. Решая характеристическое уравнение
– частное решение данного неоднородного уравнения. Решая характеристическое уравнение  , найдем его корни:
, найдем его корни: 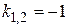 . По формуле (II.II):
. По формуле (II.II): 
Найдем частное решение неоднородного уравнения с правой частью: 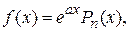
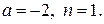 По формуле (II.IV)
По формуле (II.IV) 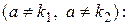
 коэффициенты А и В подлежат определению из условия, что
коэффициенты А и В подлежат определению из условия, что  решение данного уравнения. Находим производные:
решение данного уравнения. Находим производные:

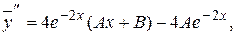
подстановка  ,
,  и
и  в уравнение дает (после сокращения на
в уравнение дает (после сокращения на  ):
):
 т.е.
т.е.  Для того, чтобы равенство было верным, достаточно совпадения коэффициентов при одних и тех же степенях
Для того, чтобы равенство было верным, достаточно совпадения коэффициентов при одних и тех же степенях  в обеих частях равенства:
в обеих частях равенства: 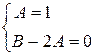
Из этих уравнений находим А= 1, В= 2. Следовательно, функция  является частным решением данного уравнения, а функция
является частным решением данного уравнения, а функция
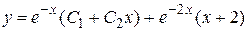 его общим решением.
его общим решением.
Пример 2. Найти общее решение уравнения: 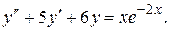
Решение. Характеристическое уравнение: 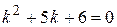 . Его корни:
. Его корни: 
 По формуле (II.I):
По формуле (II.I):  .
.
Вид правой части здесь такой же, как в примере 5, но 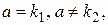 поэтому
поэтому  Следовательно,
Следовательно,
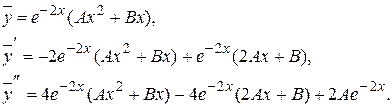
Подстановка в уравнение, сокращение на  дает:
дает: 
 ,
,  ;
;  ,
, 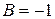 . Тогда:
. Тогда: 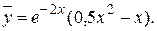
Общее решение данного уравнения  :
:

Пример 3. Найти общее решение уравнения 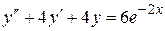 .
.
Решение. Характеристическое уравнение:  Его корни:
Его корни:  Общее решение однородного уравнения:
Общее решение однородного уравнения: 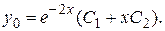 Правая часть исходного уравнения:
Правая часть исходного уравнения: 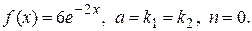 Частное решение найдем по формуле (II.IV):
Частное решение найдем по формуле (II.IV):
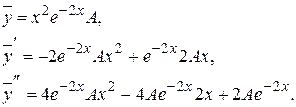
Подставим в исходное уравнение: 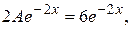

 . Тогда
. Тогда 
 .
.
Пример 4. Найти общее решение дифференциального уравнения 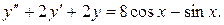
Решение. Характеристическое уравнение  имеет корни
имеет корни 
 . По формуле (II.III):
. По формуле (II.III): 

 по формуле (II.V):
по формуле (II.V):

Подстановка в дифференциальное уравнение дает:  Для того чтобы это равенство выполнялось, достаточно совпадения коэффициентов при
Для того чтобы это равенство выполнялось, достаточно совпадения коэффициентов при  в обеих частях равенства:
в обеих частях равенства:


Решая систему, получим  Тогда частное решение неоднородного уравнения:
Тогда частное решение неоднородного уравнения:  и общее решение данного уравнения
и общее решение данного уравнения 
|
|
Дата добавления: 2017-01-13; Просмотров: 210; Нарушение авторских прав?; Мы поможем в написании вашей работы!