
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод подстановки
|
|
|
|
Метод интегрирования по частям
Интегрирование тригонометрических функций
1. Интегралы вида 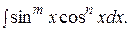 Если хотя бы одно из чисел
Если хотя бы одно из чисел  или
или  целое нечетное положительное число, то отделяя от нечетной степени один сомножитель и выражая с помощью формулы
целое нечетное положительное число, то отделяя от нечетной степени один сомножитель и выражая с помощью формулы 
оставшуюся четную степень, приходим к табличному интегралу.
Пример 1. Найти интеграл 
Решение.
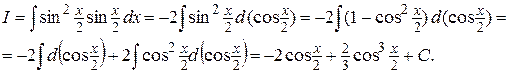
Пример 2. Найти интеграл 
Решение. 

2. Если  и
и  – четные неотрицательные числа, то используют формулы понижения степени:
– четные неотрицательные числа, то используют формулы понижения степени:

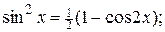

Пример 3. Найти интеграл 
Решение. 
3. Для отыскания интегралов вида  ,
, 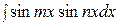 ,
,  используют следующие формулы:
используют следующие формулы:


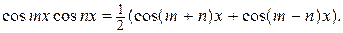
Пример 4. Найти интеграл 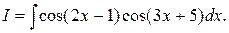
Решение. 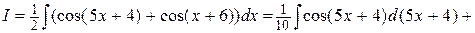

 где
где  используются формулы
используются формулы  ;
; 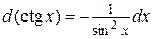 ;
; 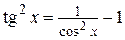 ;
;  .
.
Пример 5. Найти интеграл 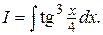
Решение.

 .
.
Если 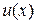 и
и 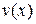 дифференцируемые функции, то справедлива формула
дифференцируемые функции, то справедлива формула 
которая называется «формулой интегрирования по частям».
Типичные интегралы, которые вычисляются по этой формуле, следующие.
1. 
 и
и 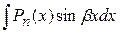 , где
, где  многочлен степени n. Целесообразно положить
многочлен степени n. Целесообразно положить 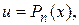 оставшуюся часть принять за
оставшуюся часть принять за  .
.
Пример 1. Найти интеграл 
Решение. 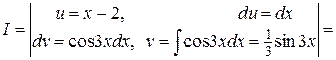

Пример 2. Найти интеграл 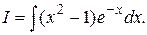
Решение. 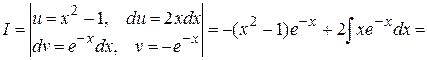

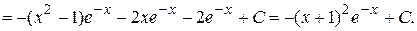
Из этих примеров видно, что интегрирование по частям можно применять несколько раз.
2. 
 ;
;  и т.п.
и т.п.
Здесь полагаем  (или
(или  , или
, или 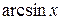 ).
).
Пример 3. Найти интеграл 
Решение. 
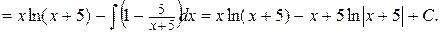
Справедливо равенство  , где
, где  –дифференцируемая функция. После вычислений интеграла надо сделать обратную подстановку
–дифференцируемая функция. После вычислений интеграла надо сделать обратную подстановку 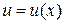 . Конечно, этим методом целесообразно пользоваться, если после подстановки интеграл упрощается.
. Конечно, этим методом целесообразно пользоваться, если после подстановки интеграл упрощается.
Пример 1. Найти интеграл 
Решение.

Выбор подстановки требует определенного опыта и искусства, но для некоторых классов функций можно дать рекомендации.
1.Интегрирование линейных иррациональностей
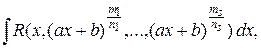 где R – рациональная функция своих аргументов. Интеграл сводится к интегрированию рациональной дроби подстановкой
где R – рациональная функция своих аргументов. Интеграл сводится к интегрированию рациональной дроби подстановкой 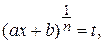 где
где 
Пример 2. Найти интеграл 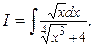
Решение. 


2. Интегрирование квадратичных иррациональностей. Тригонометрические подстановки
Интегралы вида  ,
,  ,
, 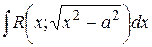 приводятся к интегралам от рациональной функции относительно
приводятся к интегралам от рациональной функции относительно 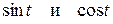 с помощью надлежащей тригонометрической подстановки: для первого интеграла
с помощью надлежащей тригонометрической подстановки: для первого интеграла  , для второго
, для второго  и для третьего
и для третьего  .
.
Пример 3. Найти интеграл 
Решение. 

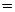

Пример 4. Найти интеграл 
Решение. 

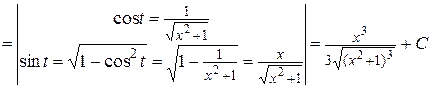 .
.
3. Универсальная тригонометрическая подстановка 
Под интегралом имеем рациональное выражение относительно 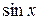 и
и  . Такие интегралы приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки
. Такие интегралы приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки  . В этом случае:
. В этом случае: 
Пример 5. Найти интеграл 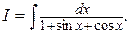
Решение. 

|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 195; Нарушение авторских прав?; Мы поможем в написании вашей работы!