
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные дифференциальные уравнения
|
|
|
|
Уравнения с разделяющимися переменными
Уравнение  будем называть уравнением с разделяющимися переменными, если
будем называть уравнением с разделяющимися переменными, если  может быть разложено на множители, каждый из которых зависит только от одной переменной:
может быть разложено на множители, каждый из которых зависит только от одной переменной:  .
.
 (II)
(II)
Производную  можно рассматривать как отношение дифференциалов:
можно рассматривать как отношение дифференциалов:  , уравнение (II) примет вид
, уравнение (II) примет вид  Умножая обе части на
Умножая обе части на  и деля на
и деля на  , приведём уравнение к виду
, приведём уравнение к виду  (переменные разделены). Интегрируя левую часть равенства по
(переменные разделены). Интегрируя левую часть равенства по  а правую часть по
а правую часть по  получаем общий интеграл (общее решение) уравнения (II):
получаем общий интеграл (общее решение) уравнения (II): 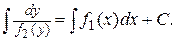
Пример. Найти общий интеграл уравнения 
Решение. Данное уравнение является уравнением с разделяющимися переменными. Запишем его в виде:  . Разделим переменные, поделив почленно на
. Разделим переменные, поделив почленно на 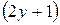 и умножив на
и умножив на 
 . Проинтегрируем:
. Проинтегрируем:  ,
, 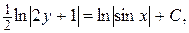
 Обозначим произвольную постоянную
Обозначим произвольную постоянную  через
через  , что допустимо, т.к.
, что допустимо, т.к.  (при
(при  ) может принимать любое значение от
) может принимать любое значение от  до
до  . Следовательно,
. Следовательно,  или
или  – общий интеграл.
– общий интеграл.
Уравнение вида  (III)
(III)
называют линейным дифференциальным уравнением. Если 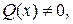 то уравнение называется линейным неоднородным, если
то уравнение называется линейным неоднородным, если  – линейным однородным.
– линейным однородным.
Линейные неоднородные уравнения могут быть решены методом Бернулли, который заключается в следующем. С помощью подстановки  где
где  и
и 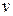 две неизвестные функции, исходное уравнение (III) преобразуется к виду
две неизвестные функции, исходное уравнение (III) преобразуется к виду
 или
или 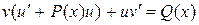 . (IV)
. (IV)
Так как одна из неизвестных функций может быть выбрана совершенно произвольно, за  выбираем любое частное решение уравнения
выбираем любое частное решение уравнения  при этом из (IV) остаётся
при этом из (IV) остаётся

Общее решение исходного уравнения находится умножением  на v:
на v:
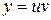 .
.
Пример. Проинтегрировать уравнение 
Решение. Данное уравнение является линейным уравнением первого порядка. Положим 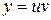 , тогда
, тогда  . Подставим
. Подставим  и
и  в данное уравнение
в данное уравнение  Сгруппируем члены, содержащие
Сгруппируем члены, содержащие 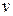 :
:  Подберём
Подберём  так, чтобы выражение в скобках обратилось в нуль:
так, чтобы выражение в скобках обратилось в нуль:  или
или  тогда
тогда  проинтегрировав, имеем
проинтегрировав, имеем  , т.е.
, т.е.  Решим оставшееся уравнение, подставив в него найденное
Решим оставшееся уравнение, подставив в него найденное 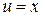 :
: 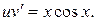

Общее решение данного уравнения имеет вид  .
.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 331; Нарушение авторских прав?; Мы поможем в написании вашей работы!