Основні теоретичні відомості

Якщо — попарно взаємно прості числа, то конгруенція

(1)

еквівалентна системі конгруенцій

(2)

Число розв'язків конгруенції (1) дорівнює де дорівнює відповідно числу розв'язків кожної з конгруенцій (2). Отже, треба розв'язати конгруенцію виду

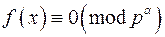(3)

де — просте число, .

Будь-який розв'язок

(4)

конгруенції

(5)

при умові, що не , є одним з розв'язків конгруенції (3).

Якщо то розв'язок (4) або не дає жодного розв'язку для (3), або дає кілька розв'язків.

Нехай розв'язок конгруенції 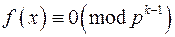Тоді число є розв'язком конгруенції тоді і тільки тоді, коли відповідне значення 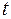задовольняє конгруенцію

. (6)

Якщо конгруенція (6) не має розв'язків, то в класі розв'язків 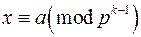конгруенції 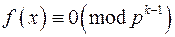немає жодного розв'язку конгруенції .

Якщо конгруенція (6) має розв'язки і , то будь-яке ціле число задовольняє конгруенцію (6), а тому є розв'язками (6). Тоді клас розв'язків 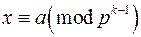конгруенції 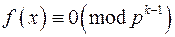дає розв'язків конгруенції , а саме: , , ,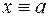

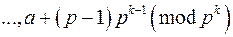
Якщо конгруенція (6) має розв'язки і не ділиться на , то це є

єдиний розв'язок . Тоді з класу розв'язків 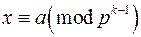конгруенції 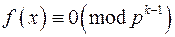дістаємо єдиний розв'язок 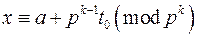конгруенції .

Конгруенцію (5) завжди можна замінити еквівалентною конгруенцією того самого степеня із старшим коефіцієнтом, що дорівнює одиниці. Для цього слід обидві частини конгруенції (5) помножити на число ,яке задовольняє конгруенцію . Це число визначається однозначно, оскільки .

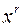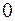Конгруенцію (5) можна замінити еквівалентною їй конгруенцією степеня не вище за тим самим модулем (згідно з теоремою про пониження степеня конгруенції). Для цього треба в конгруенції (5) замінити вираз на , де — остача від ділення на . Ділення на можна фактично й не виконувати, а просто замінювати кожне у лівій частині (5) на , де — остача від ділення на при умові, що остачу замінюємо числом .

Якщо 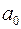не ділиться на , то конгруенція (5) степеня має не більш ніж різних розв'язків.

Конгруенція (5) має більш як розв'язків тоді і тільки тоді, коли всі коефіцієнти в лівій частині 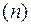діляться на , тобто коли конгруенція тотожна.

Конгруенція (5) степеня , в якій , , 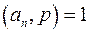має розв'язків тоді і тільки тоді, коли всі коефіцієнти остачі від ділення на діляться на .

Теорема Вільсона. Натуральне число тоді і тільки тоді є простим, коли .

Якщо — просте число, то конгруенція

має точно розв'язок.

Якщо — просте число і — натуральний дільник числа , то конгруенція

має точно розв'язків.

Методичні рекомендації до розв‘язування задач

Приклад 1. Розв‘язати конгруенцію

.

Розв‘язання. Замінимо цю конгруенцію еквівалентною їй конгруенцією степеня не вище 6 за тим самим модулем 7. Поділимо на 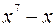. Дістанемо

.

Розв‘яжемо конгруенцію . Штучним способом знаходимо ,

,

.

Отже, дана конгруенція має єдиний розв‘язок .

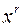Зауваження. Замість того, щоб ділити на , можна бу3лоб замінити на , де остача від ділення на , причому. якщо ділиться на , то покладемо .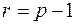

Приклад 2. Розв‘язати конгруенцію

.

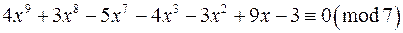Так як степінь многочлена більший модуля, застосувавши вище вказане зауваження, одержимо: , , . Тоді дана конгруенція буде еквівалентна такій:

,

,

,

.

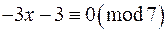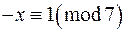Отже, розв‘язок даної конгруенції .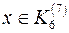

Приклад 3. Розв‘язати конгруенцію

.

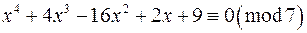Розв‘язання. Випробовуючи абсолютно найменші лишки за модулем 7, а саме: , знайдемо перший розв‘язок даної конгруенції

.

Одержуємо, за теоремою 23, дана конгруенція буде тотожна конгруенції

.

Позначимо . Замінимо коефіцієнти на абсолютно найменші за модулем 7. .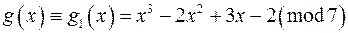

Випробуємо далі абсолютно найменші лишки за модулем 7 стосовно многочлена .

.

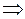
, де .

Аналогічно випробуємо абсолютно найменші лишки за модулем 7 для многочлена .

,

,

,

,

,

.

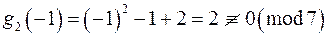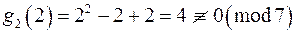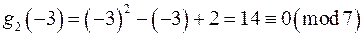Отже, дана конгруенція має два розв‘язки, а саме: .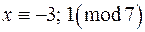

Приклад 4. Розв‘язати конгруенцію

.

Розв‘язання. Оскільки , то задана конгруенція еквівалентна системі конгруенцій за простими модулями:

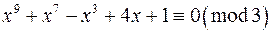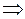
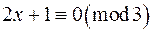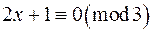Розв‘язуємо окремо кожну з конгруенцій. За теоремою Б, , , , . . Так як , то конгруенція має єдиний розв‘язок. , , .

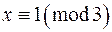За теоремою Б , . , , .

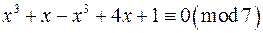
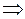
Розв‘язуючи тепер спільно конгруенці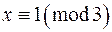ї і , дістанемо їхній спільний розв‘язок:

.

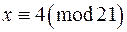Це і буде єдиним розв‘язком цієї конгруенції.

Приклад 5. Розв‘язати конгруенцію

.

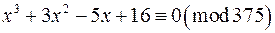Розв‘язання. Оскільки 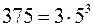, то задана конгруенція еквівалентна системі

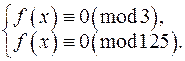
Перша з цих конгруенцій після спрощення матиме вигляд

.

Остання конгруенція, а отже, і конгруенція , матиме єдиний розв‘язок .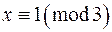

Щоб розв‘язати другу конгруенцію системи, треба спочатку розв‘язати конгруенцію

,

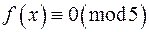або після спрощення

. (*)

Методом проб, підставляючи послідовно абсолютно найменші лишки за модулем 5 , знаходимо розв‘язки конгруенції (*).

, .

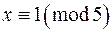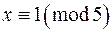Випробуємо . У класі беремо числа , де задовольняє співвідношення або .

Оскільки , , , то , тобто , або , .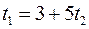

Дістаємо .

Знаходимо далі , і розв‘язуємо конгруенцію або .

,

,

звідки 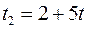, де . Тоді .

Випробуємо клас 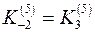. У класі 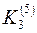беремо числа 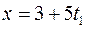, де задовольняє співвідношення 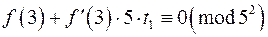або .

Оскільки , , то . Остання конгруенція не має розв‘язку, так як , а . Отже, конгруенція має один розв‘язок ,

Таким чином, щоб знайти розв‘язки даної конгруенції, треба розв‘язати тільки одну систему:

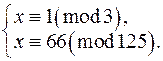
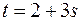, , , , , де . .

Відповідь: .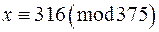

Задачі рекомендовані до розв‘язування в аудиторії

1. Звести задані конгруенції до еквівалентних їм конгруенцій, степінь яких менше за модуль, а старший коефіцієнт дорівнює 1:

а) ;

б) ;

в)

;

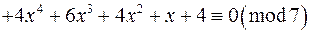г) .

2. Спростити задані конгруенції (понизити степені, зменшивши коефіцієнти за абсолютною величиною, зробити так, щоб старший коефіцієнт дорівнював 1) і розв‘язати способом підбору:

а) ;

б) ;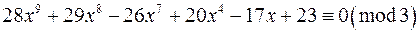

в) ;

г) .

3. Спростити задані конгруенції і розв‘язати їх способом підбору:

а) ;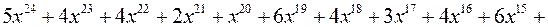

б) ;

в) ;

г) .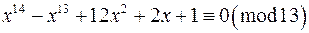

4. Розкласти конгруенції на лінійні множники за даним модулем:

а) ;

б) ;

в) ;

г) .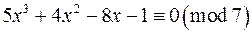

5. Розв‘язати конгруенції:

а) ;

б) ;

в) ;

г) ;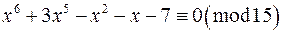

д) ;

е) .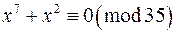

Задачі рекомендовані до розв‘язування дома

1. Звести задані конгруенції до еквівалентних їм конгруенцій, степінь яких менше за модуль, а старший коефіцієнт дорівнює 1:

а)

б) ;

в) ;

г) .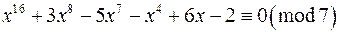

2. Спростити задані конгруенції (понизити степені, зменшивши коефіцієнти за абсолютною величиною, зробити так, щоб старший коефіцієнт дорівнював 1) і розв‘язати способом підбору:

а) ;

б) ;

в) ;

в) .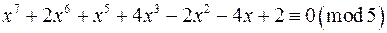

3. Спростити задані конгруенції і розв‘язати їх способом підбору:

а) ;

б) ;

в) ;

г) ;

д) .

4. Розкласти конгруенції на лінійні множники за даним модулем:

а) ;

б) ;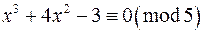

в) ;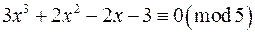

г) ;

д) .

5. Розв‘язати конгруенції:

а) ;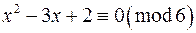

б) ;

в) ;

г) ;

д) .

Модуль 3

Практичне заняття 2

Конгруенції другого степеня. Зведення до двочленної конгруенції.

Квадратичні лишки і нелишки. Символ Лежандра

Дата добавления: 2017-02-01