Основні теоретичні відомості 2 страница

Найбільший спільний дільник заданих многочленів визначається однозначно з точністю до сталого множника.

Для будь-яких двох многочленів і з кільця (з яких хоча б один відмінний від 0) існує найбільший спільний дільник, який дорівнює останній відмінній від нуля остачі в алгоритмі Евкліда.

Найбільший спільний дільник многочленів і з кільця завжди можна подати у вигляді

де 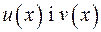- деякі многочлени з кільця .

Многочлени називаються взаємно простими, якщо кожен їхній спільний дільник є многочленом нульового степеня. При цьому пишуть

Многочлени і з кільця є взаємно простими тоді і тільки тоді, коли існують многочлени такі, що

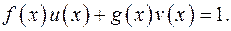
Взаємно прості многочлени мають такі властивості:

Спільним кратним многочленів і з кільця називають многочлен такий, що ділиться на і . Найменшим спільним кратним многочленів і називається таке їхнє спільне кратне, на яке ділиться кожне спільне кратне цих многочленів.

Найменше спільне кратне многочленів і визначається однозначно з точністю до сталого множника і позначається через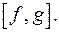

Для довільних відмінних від нуля многочленів і з кільця найменше спільне кратне існує в і визначається за формулою

Приклад 1. Знайти числа та , при яких многочлен ділиться на многочлен якщо

Розв’язання. Многочлен має степінь 4; позначимо 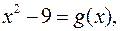його степінь – 2. Тому степінь шуканого многочлена (якщо він існує) дорівнює 2. Нехай

і тоді

З умови рівності многочленів маємо систему рівнянь:

Відповідь: Многочлен ділиться на многочлен при .

Приклад 2. Виконати ділення многочлена

на

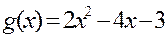
в кільці

Розв’язання. Застосуємо табличну схему. В таблиці повинно бути 9 стовпців і 8 рядків. Маємо:

стовпців

рядків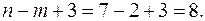

		-36			-6		-20	-13
		-20	-15
-4		-16
			-4
					-12	-9
							-24	-18
		-8	-2-

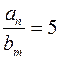
Відповідь:

Приклад 3. Виконати ділення многочлена

на в кільці .

Розв‘язання. Маємо: , тоді стовпців

рядків

			-6			-4
		-10
-5			-25

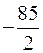
Відповідь:

Приклад 4. Знайти найбільший спільний дільник многочленів

і

над полем раціональних чисел.

Розв’язання. Щоб уникнути дробових коефіцієнтів, помножимо попередньо на 3:

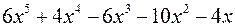
Тепер, щоб уникнути дробових коефіцієнтів, помножимо одержану різницю на 3. В даному випадку остача визначиться з точністю до множника нульового степеня.

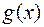Таким чином, ми знайшли з точністю до множника нульового степеня остачу від ділення на Тепер потрібно ділити на Ми можемо впевнитися, що 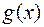ділиться без остачі на Отже, і є найбільший спільний дільник многочленів і

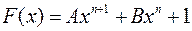Приклад 5. Визначити так, щоб многочлен ділився на

Розв’язання.

				…
				…
				…

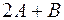
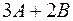
Щоб 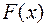ділився на потрібно, щоб остачі і дорівнювали нулю. З цієї умови і знаходимо :

Звідси

Такими будуть наприклад, многочлени:

для

для і так далі.

[Костарчук В. Н. Высшая алгебра Часть ІІ. Алгебра многочленов.]

Приклад 6. При яких значеннях многочлен ділиться без остачі на

Розв’язання. За теоремою Безу тобто

Відповідь: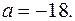

Приклад 7. Знайти найбільший спільний дільник многочленів та визначити многочлени 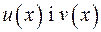такі, щоб виконувалась рівність: якщо:

Розв‘язання. І крок

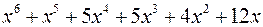
Таким чином

ІІ крок. Поділимо на

ІІІ крок. Поділимо на

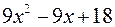
ІV крок. Поділимо на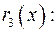

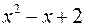
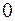
Так як то передостання остача в алгоритмі Евкліда буде найбільшим спільним дільником многочленів .

Із (3) знаходимо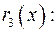

Із (2) виразимо

Із (1) виразимо через

Відповідь:

Приклад 8. Розділити многочлен 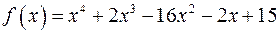на двочлен

Розв’язання. Виконаємо ділення многочлена на двочлен за схемою Горнера:

			-16	-2
			-8	-18	-21

Отже, частка дорівнює а остача

Приклад 9. Розкласти многочлен за степенями двочлена

Розв’язання. Складемо таблицю:

		-5		-2
		-3	-3	-8
		-1	-5
		1
	1

У першому рядку цієї таблиці стоять коефіцієнти даного многочлена ; у другому рядку маємо результат ділення на і остачу у третьому рядку маємо вже результат ділення на і остачу що утворилась при цьому діленні, і так далі.

Отже, виділені у таблиці числа 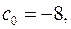є коефіцієнтами шуканого многочлена:

Приклад 10. Обчислити з точністю до 0,0 01 значення многочлена при

Розв’язання. Розкладемо даний многочлен за степенями двочлена

			-2
			-1

Якщо то

Відповідь: 1,997027.

Приклад 11. Знайти такі пари многочленів 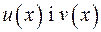в кільці що де

Розв’язання. В кільці нам необхідно розв’язати рівняння 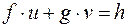(1) з невідомими . Нехай Якщо існує хоча б один розв’язок то 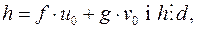так як Нехай Так як многочлен лінійно зображується через многочлени 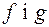, тобто то 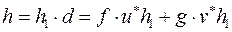, тобто пара многочленів 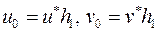- розв’язок нашого рівняння (1). Таким чином умова 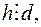необхідна і достатня для існування розв’язку рівняння (1).

Дата добавления: 2017-02-01