
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами.
|
|
|
|
Якщо коефіцієнти  многочлена
многочлена  в кільця
в кільця  діляться на деяке просте число
діляться на деяке просте число  , причому
, причому  не ділиться на
не ділиться на  а старший коефіцієнт
а старший коефіцієнт 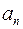 не ділиться на
не ділиться на  , то многочлен
, то многочлен  незвідний у полі раціональних чисел.
незвідний у полі раціональних чисел.
Отже, у кільці многочленів над полем раціональних чисел є многочлени довільного степеня, які незвідні у полі 
Нехай  - деяке числове поле. Число
- деяке числове поле. Число  називають алгебраїчним відносно поля
називають алгебраїчним відносно поля  , якщо воно є коренем деякого многочлена над полем
, якщо воно є коренем деякого многочлена над полем  . Число, яке не є алгебраїчним відносно поля
. Число, яке не є алгебраїчним відносно поля  , називають трансцендентним відносно
, називають трансцендентним відносно  . Зокрема, алгебраїчні і трансцендентні числа і відносно поля раціональних чисел
. Зокрема, алгебраїчні і трансцендентні числа і відносно поля раціональних чисел 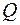 називають відповідно просто алгебраїчним і трансцендентними.
називають відповідно просто алгебраїчним і трансцендентними.
Якщо  є алгебраїчним числом відносно поля
є алгебраїчним числом відносно поля  , то в кільці
, то в кільці  існує єдиний незвідний зведений многочлен
існує єдиний незвідний зведений многочлен  , який має
, який має  своїм коренем, а його степінь
своїм коренем, а його степінь  є найменшим серед степенів усіх многочленів з коренем
є найменшим серед степенів усіх многочленів з коренем  . При цьому многочлен
. При цьому многочлен  називають мінімальним многочленом числа
називають мінімальним многочленом числа  , а його степні
, а його степні  - степенем алгебраїчного числа
- степенем алгебраїчного числа  відносно поля
відносно поля  .
.
Мінімальне розширення поля  , яке містить число
, яке містить число  називають простим розширенням поля
називають простим розширенням поля  , утвореним приєднанням числа
, утвореним приєднанням числа  , і позначають через
, і позначають через  . Якщо
. Якщо  є алгебраїчним (трансцендентним) відносно поля
є алгебраїчним (трансцендентним) відносно поля  , то
, то  називають простим алгебраїчним (трансцендентним) розширенням.
називають простим алгебраїчним (трансцендентним) розширенням.
Поле  , утворене з поля
, утворене з поля  приєднанням кореня
приєднанням кореня  незвідного у полі
незвідного у полі  многочлена
многочлена  -го степеня
-го степеня

Складається з усіх чисел виду

де 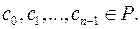
Нехай  - деяке підполе поля
- деяке підполе поля  . Тоді
. Тоді  можна розглядати як векторний простір над полем
можна розглядати як векторний простір над полем  . При цьому розширення
. При цьому розширення  поля
поля  називають скінченим, якщо
називають скінченим, якщо  є скінченно-вимірним векторним простором над
є скінченно-вимірним векторним простором над  . При цьому розмірність простору
. При цьому розмірність простору  називають степенем розширення
називають степенем розширення  над полем
над полем  .
.
Просте алгебраїчне розширення  є скінченним розширенням поля
є скінченним розширенням поля  , а степінь розширення
, а степінь розширення  над полем
над полем  дорівнює степеню числа
дорівнює степеню числа  відносно
відносно  .
.
Розширення  поля
поля  , утворене за допомогою кількох послідовно виконаних простих алгебраїчних розширень, називають складеним алгебраїчним розширенням. Розширення
, утворене за допомогою кількох послідовно виконаних простих алгебраїчних розширень, називають складеним алгебраїчним розширенням. Розширення  поля
поля  називають алгебраїчним, якщо всі його елементи є алгебраїчними відносно поля
називають алгебраїчним, якщо всі його елементи є алгебраїчними відносно поля  .
.
Будь-яке скінченне розширення поля  є його алгебраїчним та складеним розширенням. Кожне складене алгебраїчне розширення поля
є його алгебраїчним та складеним розширенням. Кожне складене алгебраїчне розширення поля  є простим розширенням цього поля.
є простим розширенням цього поля.
Методичні рекомендації до розв‘язування задач
Приклад 1. Розв‘язати рівняння
 .
.
Розв‘язання. Знайдемо спочатку раціональні корені цього рівняння (якщо вони є). Раціональними коренями тут можуть бути такі числа:
 (*)
(*)
Знайдемо межі дійсних коренів заданого рівняння. Оскільки  і
і 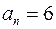 , то
, то  . Отже, всі дійсні корені знаходяться в інтервалі
. Отже, всі дійсні корені знаходяться в інтервалі  . Серед чисел ряду (*) у цей інтервал входять такі числа:
. Серед чисел ряду (*) у цей інтервал входять такі числа:
 (**)
(**)
Для заданого рівняння маємо:  і
і  . Поставимо умову, щоб числа
. Поставимо умову, щоб числа  були цілими. Тоді залишаться числа:
були цілими. Тоді залишаться числа:
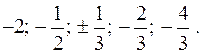 (***)
(***)
Так як  , то 1 є корінь рівняння.
, то 1 є корінь рівняння.
Застосуємо схему Горнера для перевірки того, яке з чисел ряду (***) є коренем заданого рівняння.
| – 7 | – 12 | – 4 | |||||
| – 2 | |||||||
– 
| |||||||
– 
| 
| 
| |||||
– 
| |||||||

|  4 4
| 
| |||||
– 
| – 8 | 
|
У схемі виділено коефіцієнти повних часток. отже, задане рівняння має чотири раціональних корені:  . Решту коренів рівняння знайдемо, прирівнюючи останню частку до нуля. Матимемо:
. Решту коренів рівняння знайдемо, прирівнюючи останню частку до нуля. Матимемо:

 .
.
У цьому рівнянні комплексні корені  . Тому задане рівняння має шість різних коренів:
. Тому задане рівняння має шість різних коренів:  .
.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 143; Нарушение авторских прав?; Мы поможем в написании вашей работы!