Кубічні рівняння

Загальний вигляд кубічного рівняння такий:

.

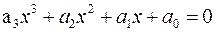
Поділимо дане рівняння на 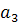, дістанемо рівняння

,

старший коефіцієнт якого рівний 1, тобто зведене рівняння.

Нехай дано кубічне рівняння

(1)

з будь-якими комплексними коефіцієнтами.

Щоб позбутися у рівнянні (1) члена з невідомим у другому степені, виконаємо підстановку

Тоді дістанемо рівняння

(2)

Отже, щоб розв’язати рівняння (1), досить уміти розв’язувати «неповне» кубічне рівняння

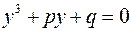(3)

з будь-якими комплексними коефіцієнтами. Розглянемо один з кількох відомих способів розв’язувати рівняння (3). Запишемо невідоме у вигляді суми , де u і v- нові невідомі, і підставимо цей вираз у рівняння (3).

Дістанемо:

.

Або, після розкриття дужок і перегрупування членів:

.

Якщо u і v вибрати так, щоб

.

(4)

то тоді буде коренем рівняння (3). Але якщо для u і v справджуватимуться рівності (4), то справджуватимуться і рівності

,

(5)

Тому і за формулами Вієта для коренів квадратного рівняння будуть коренями квадратного рівняння

.

Нехай

Тоді

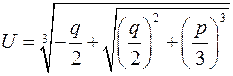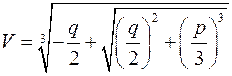, .(6)

Відповідно до цього

(7)

Це і є формула коренів кубічного рівняння, яку називають формулою Кардано.

Кубічний корінь з будь-якого комплексного числа, відмінного від нуля, має в полі комплексних чисел три значення. Отже, і мають по три значення.

Може виникнути думка, що комбінуючи три значення u з трьома значеннями v, дістанемо дев’ять різних значень y за формулою (2)

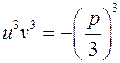Проте не слід забувати, що система (5), яку ми фактично розв’язували, не рівносильна системі (4), бо рівність замінена рівністю . Внаслідок цього не всі розв’язки системи (5) будуть розв’язками системи (4). Тому слід вибрати лише ті значення коренів (6), які задовольняють друге з рівнянь (4), тобто умову (8)

Застосовуючи формулу Кардано, знаходять значення одного з радикалів, а відповідні їм значення другого радикала визначають, користаючи співвідношенням (8), і таким чином, знаходять усі корені рівняння (3).

Спинимося на цьому питанні докладніше.

Нехай - будь-яке одне з трьох значень u. Тоді два інших значення u можна дістати множенням на кубічні корені і з одиниці.

Отж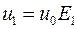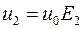е: , , де

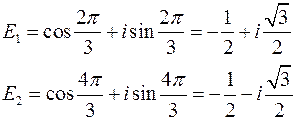
Позначимо символом те з трьох значень радикала V, яке відповідає значення радикала u.

із співвідношення (8):

.

Двома іншими значеннями V будуть 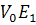і . Значенню відповідатиме значення радикала , бо .

Так само легко переконатися, що значення 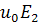радикала відповідатиме значення 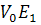радикала V. Додаючи відповідні значення і , дістанемо три корені рівняння (2)

(9)

Отже, кожне кубічне рівняння з будь-якими числовими коефіцієнтам в полі комплексних чисел має три корені.

Дата добавления: 2017-02-01