
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кубічні рівняння з дійсними коефіцієнтами в полі комплексних чисел
|
|
|
|
Нехай дано неповне кубічне рівняння:
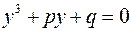 (10)
(10)
з дійсними коефіцієнтами. З’ясуємо, що можна сказати про корені цього рівняння. У цьому випадку вираз 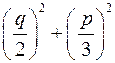 , що стоїть у формулі Кардано під знаком квадратного кореня, є дійсне число. Вираз
, що стоїть у формулі Кардано під знаком квадратного кореня, є дійсне число. Вираз  називається дискримінантом кубічного рівняння. (10). Цей дискримінант може бути додатним, дорівнювати нулю або бути від’ємним. Розглянемо кожну з цих можливостей.
називається дискримінантом кубічного рівняння. (10). Цей дискримінант може бути додатним, дорівнювати нулю або бути від’ємним. Розглянемо кожну з цих можливостей.
1.Нехай  . У цьому випадку у формулі Кардано під знаком кожного з квадратних коренів стоїть додатне число, а тому під знаком кожного з кубічних коренів стоїть дійсне число. Отже, кожен з кубічних коренів u і v матиме одне дійсне значення й два –комплексні спряжені.
. У цьому випадку у формулі Кардано під знаком кожного з квадратних коренів стоїть додатне число, а тому під знаком кожного з кубічних коренів стоїть дійсне число. Отже, кожен з кубічних коренів u і v матиме одне дійсне значення й два –комплексні спряжені.
Позначимо символом  дійсне значення радикала u. Тоді відповідне йому значення
дійсне значення радикала u. Тоді відповідне йому значення  радикала v також буде дійсним, оскільки добуток
радикала v також буде дійсним, оскільки добуток  повинен дорівнювати
повинен дорівнювати  .
.
Таким чином корінь

Рівняння (10) буде дійсним числом. Два інші корені цього рівняння знайдемо за формулами (9):
 Оскільки
Оскільки  є дійсні значення різних кубічних радикалів, то
є дійсні значення різних кубічних радикалів, то 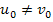 ,
,
і таким чином, корені  є спряженими комплексними числами.
є спряженими комплексними числами.
Отже, якщо  то рівняння (10) має один дійсний і два комплексні спряжені корені.
то рівняння (10) має один дійсний і два комплексні спряжені корені.
2.Нехай 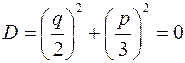 .У цьому випадку
.У цьому випадку
 ,
,  .
.
Нехай  – дійсне значення радикала U. Відповідні йому значення
– дійсне значення радикала U. Відповідні йому значення  радикала V також є дісним числом, бо
радикала V також є дісним числом, бо  . Але оскільки
. Але оскільки 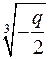
має лише одне дійсне значення, то 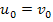 . Тому
. Тому
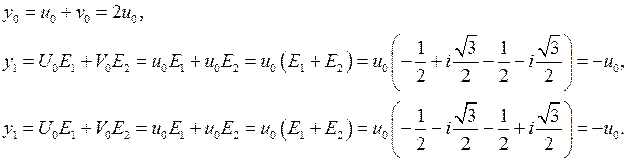 Отже, якщо
Отже, якщо 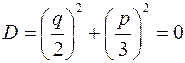 , то всі корені рівняння (10) дійсні, причому два з них рівні між собою.
, то всі корені рівняння (10) дійсні, причому два з них рівні між собою.
3.Нехай  . У цьому випадку в формулі Кардано під знаком кожного з квадратних радикалів стоїть дійсне від’ємне число. Отже, під знаком кубічних радикалів стоятимуть u і v стоятимуть комплексні числа, а тому всі значення радикалів u і v будуть комплексними числа.
. У цьому випадку в формулі Кардано під знаком кожного з квадратних радикалів стоїть дійсне від’ємне число. Отже, під знаком кубічних радикалів стоятимуть u і v стоятимуть комплексні числа, а тому всі значення радикалів u і v будуть комплексними числа.
Покажемо, що в цьому випадку у формулі Кардано значення радикала v повинно бути спряжене відповідному значенню радикала u. Нехай  -,будь-яке із значень радикала u, а
-,будь-яке із значень радикала u, а  відповідне йому значення радикала v. Тоді відповідно до правила добування кореня n-го степеня:
відповідне йому значення радикала v. Тоді відповідно до правила добування кореня n-го степеня:
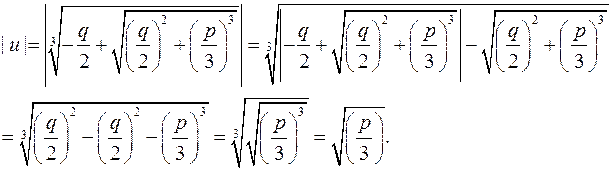 і тому
і тому
 .
.
Тобто

Таким чином, за формулами (9)
 Як бачимо, у цьому випадку рівняння (10) має три різні дійсні корені.
Як бачимо, у цьому випадку рівняння (10) має три різні дійсні корені.
Останній випадок переконливо доводить, що практична цінність формули Кардано невелика. Справді, хоч у цьому випадку всі корені рівняння з дійсними коефіцієнтами дійсні, проте відшукання їх за формулою Кардано вимагає добування кубічного кореня з комплексного числа, для чого треба записувати ці числа в тригонометричній формі. Отже, запис коренів кубічного рівняння за допомогою радикалів втрачає практичне значення.
Приклад. Розв’язати рівняння  .
.
Розв’язання

Отже, ми маємо незвідний випадок. Радикал у цьому випадку записується так:

Щоб добути кубічний корінь з комплексного числа  , запишемо це число в тригонометричній формі. Знайдемо його модуль ρ і його аргумент γ:
, запишемо це число в тригонометричній формі. Знайдемо його модуль ρ і його аргумент γ:
 .
.
 ,
, 

 .
.
Звідси
 .
.
І за формулами (6)
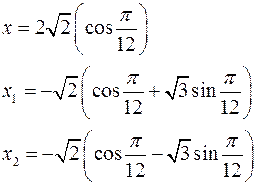 .
.
Застосовуючи формули ділення аргументу пополам, знаходимо:
 .
.
Підставивши знайдені значення  і
і  у записані вище рівності, матимемо:
у записані вище рівності, матимемо:
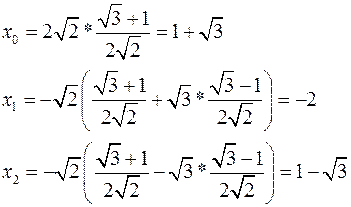
Відповідь:  .
.
Приклад 2. Розв’язати рівняння  .
.
Приклад 3. Розв’язати рівняння  .
.
Приклад 4. Розв’язати рівняння 
Розв’язання:
Підстановка  зводить рівняння до виду:
зводить рівняння до виду:
 .
.
Тут 
 .
.
Тобто дане рівняння має один дійсний корінь і два комплексні спряжені:
 ,
,
 .
.
Тоді 
 .
.
Два інших корені знайдемо за формулою (9)
 .
.
У відповідності з підстановкою, знаходимо:
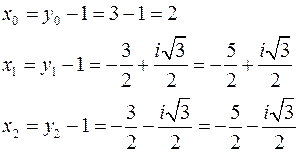
Відповідь:  .
.
Задачі рекомендовані для розв‘язання аудиторії
1. Знайти раціональні корені многочленів:
а) 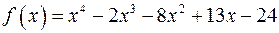 ;
;
б)  ;.
;.
в)  ;
;
г)  ;
;
д) 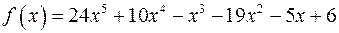 .
.
2. Розв’язати рівняння:
а)  ; б)
; б)  .
.
в)  ; г)
; г) 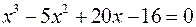 .
.
д)  ; е)
; е)  ;
;
є) 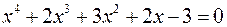 ; ж)
; ж)  .
.
Задачі рекомендовані для розв‘язання дома
1. Знайти раціональні корені многочленів:
а)  ;
;
б) 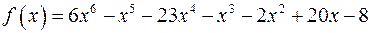 ;
;
в) 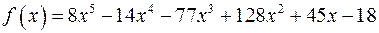 ;
;
г) 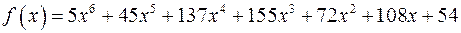 ;
;
д) 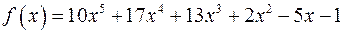 ;
;
е) 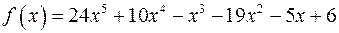 .
.
2. Розв’язати рівняння:
а) 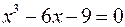 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
д) 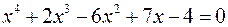 ; е)
; е)  ;
;
є) 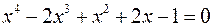 ; ж)
; ж)  .
.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 147; Нарушение авторских прав?; Мы поможем в написании вашей работы!