
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні теоретичні відомості
|
|
|
|
Для будь-якого поля  існує (з точністю до ізоморфізму) поле
існує (з точністю до ізоморфізму) поле  , яке містить кільце
, яке містить кільце  многочленів над полем
многочленів над полем  і кожен елемент якого можна подати як частку
і кожен елемент якого можна подати як частку
 , де
, де 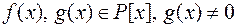 . (1)
. (1)
Зауважимо, що відповідно до загальної теорії елементом поля  є не кожна окрема частина (1), а клас часток, які дорівнюють одна одній.
є не кожна окрема частина (1), а клас часток, які дорівнюють одна одній.
Дві частки  дорівнюють одна одній, якщо
дорівнюють одна одній, якщо
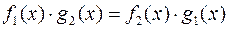 . Як правило, раціональний дріб подають часткою
. Як правило, раціональний дріб подають часткою  , для якої
, для якої 
Нехай раціональні дроби задано нескоротними частками і старший коефіцієнт знаменника дорівнює 1.
Раціональний дріб  називається правильним, якщо степінь
називається правильним, якщо степінь  менше степеня
менше степеня 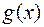 . У противному разі раціональний дріб називається неправильним.
. У противному разі раціональний дріб називається неправильним.
Елементарним дробом над полем  називається раціональний дріб виду
називається раціональний дріб виду  де
де 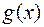 - незвідний многочлен над полем
- незвідний многочлен над полем  ,
, 
Якщо  - правильний раціональний дріб над полем
- правильний раціональний дріб над полем  і многочлени
і многочлени  - попарно взаємно прості, то в кільці
- попарно взаємно прості, то в кільці  існують многочлени
існують многочлени  такі, що
такі, що

і кожен з дробів у правій частині є правильним.
Правильний дріб над полем  виду
виду  де
де 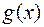 - незвідний над
- незвідний над  многочлен і
многочлен і  можна подати як суму елементарних дробів над цим полем.
можна подати як суму елементарних дробів над цим полем.
 .
.
Правильні дроби над полем  можна подати як суму елементарних дробів над цим полем і до того єдиним способом.
можна подати як суму елементарних дробів над цим полем і до того єдиним способом.
Неправильний дріб  можна подати як суму многочлена і правильного дробу.
можна подати як суму многочлена і правильного дробу.
Основна теорема теорії многочленів
Теорема. Довільний многочлен ненульового степеня з комплексними коефіцієнтами
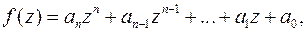
має хоча б один комплексний корінь.
Методичні рекомендації до розв’язування задач
Приклад 1. Розкласти в суму простіших дробів дійсний правильний дріб  , де
, де

Легко перевірити, що  причому кожний із многочленів
причому кожний із многочленів 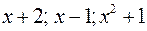 незвідний. Шуканий розклад повинен мати вигляд
незвідний. Шуканий розклад повинен мати вигляд
 (1)
(1)
де числа  треба ще знайти.
треба ще знайти.
Многочлен  можна розкласти:
можна розкласти:
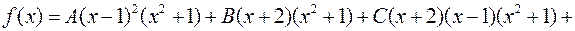
 (2)
(2)
Прирівнюючи коефіцієнти при однакових степенях невідомого  із обох частин рівності (2), ми отримали б систему із п’яти лінійних рівнянь відносно п’яти невідомих
із обох частин рівності (2), ми отримали б систему із п’яти лінійних рівнянь відносно п’яти невідомих  , при чому, ця система має рішення і притому лише одне. Ми підемо, однак, іншим шляхом.
, при чому, ця система має рішення і притому лише одне. Ми підемо, однак, іншим шляхом.
Нехай у рівності (2)  , тоді маємо, що
, тоді маємо, що  звідки
звідки  (3)
(3)
Ставлячи, в (2)  , ми отримаємо
, ми отримаємо  , тобто
, тобто  (4)
(4)
Після цього підставимо в рівність (2) послідовно  Використовуючи (6) і (7), ми отримаємо рівняння
Використовуючи (6) і (7), ми отримаємо рівняння
 (5)
(5)
Звідси 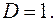 (6). Підставимо в рівність (2)
(6). Підставимо в рівність (2)  Використовуючи (3), (4) і (5), ми прийдемо до рівняння
Використовуючи (3), (4) і (5), ми прийдемо до рівняння  яке разом з першим із рівнянь (8) дає
яке разом з першим із рівнянь (8) дає 
Таким чином,

Задачі рекомендовані до розв‘язування в аудиторії
І. Розкладіть вирази на прості дроби над полем 
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4. 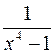 ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8. 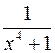 ;
;
9.  ; 10.
; 10.  .
.
Задачі рекомендовані до розв‘язування в аудиторії
І. Розкладіть вирази на прості дроби над полем 
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7. 
ІІ. Розкладіть 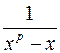 на прості дроби над полем
на прості дроби над полем 
Модуль 4
Практичне заняття 5
Цілі і раціональні корені многочлена з цілими коефіцієнтами.
Критерій Ейзенштейна. Алгебраїчні і трансцендентні числа.
Будова простого алгебраїчного розширення поля
Нехай  - многочлен з цілими коефіцієнтами.
- многочлен з цілими коефіцієнтами.
Якщо нескоротній дріб 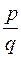 є коренем многочлена
є коренем многочлена  , то
, то  є дільником вільного члена
є дільником вільного члена  , а
, а  - дільником старшого коефіцієнта
- дільником старшого коефіцієнта 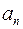 цього многочлена.
цього многочлена.
Якщо  , то раціональні корені многочлена
, то раціональні корені многочлена  є цілими числами. Оскільки многочлени
є цілими числами. Оскільки многочлени  і
і  мають однакові корені, то знаходження раціональних коренів многочлена
мають однакові корені, то знаходження раціональних коренів многочлена  можна за допомогою заміни
можна за допомогою заміни  звести до відшукання цілих коренів многочлена.
звести до відшукання цілих коренів многочлена.

Існують інші необхідні умови для того, щоб раціональне число було коренем многочлена з цілими коефіцієнтами. Зокрема, щоб нескоротний дріб 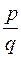 був раціональним коренем многочлена
був раціональним коренем многочлена  , необхідно, щоб при довільному цілому
, необхідно, щоб при довільному цілому 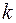 число
число 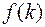 ділилося на
ділилося на  де
де  Така умова на практиці найчастіше використовується для
Така умова на практиці найчастіше використовується для  , при цьому числа
, при цьому числа  мають бути цілими.
мають бути цілими.
Многочлен  з цілими коефіцієнтами є звідним у полі
з цілими коефіцієнтами є звідним у полі 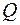 раціональних чисел тоді і тільки тоді, коли існують многочлени
раціональних чисел тоді і тільки тоді, коли існують многочлени  ненульового степеня з цілими коефіцієнтами такі, що
ненульового степеня з цілими коефіцієнтами такі, що  тобто коли многочлен
тобто коли многочлен  є звідним у кільці
є звідним у кільці 
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 69; Нарушение авторских прав?; Мы поможем в написании вашей работы!