
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні властивості індексів
|
|
|
|
1°. Усі індекси числа  за простим модулем
за простим модулем  утворюють клас чисел за модулем
утворюють клас чисел за модулем  . Точніше, якщо
. Точніше, якщо  і
і  — індекси числа
— індекси числа  за модулем
за модулем  (при будь-якій тій самій основі), то
(при будь-якій тій самій основі), то
 .
.
2°. Для того щоб  , необхідно і достатньо, щоб
, необхідно і достатньо, щоб
 .
.
Якщо значення чисел або індексів виходять за межі таблиць, то ці дві властивості дають змогу переходити до найменших невід'ємних лишків: для чисел — за модулем  , для індексів — за модулем
, для індексів — за модулем  ;
;
3°.  ;
;
4°. 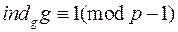 ;
;
5°.  ;
;
6°. 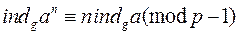 ;
;
7°. Якщо  , то
, то  .
.
Зазначимо, що перехід від конгруенції між числами до конгруенції їхніх індексів називається індексацією, а зворотний перехід – потенціюванням. Якщо задано двочленну конгруенцію
 го степеня за простим модулем
го степеня за простим модулем
 ,
,  ,
,  (5)
(5)
то її розв'язок знаходять з конгруенції
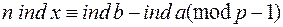 (6)
(6)
Задачі рекомендовані для розв‘язування в аудиторії
1. Знайти порядок числа  за модулем
за модулем  , якщо:
, якщо:
а)  ; б)
; б) 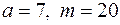 ;
;
в) 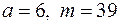 ; г)
; г)  .
.
2. Знайти порядки чисел  за модулем
за модулем  , якщо:
, якщо:
а)  ;
;
б)  ;
;
в) 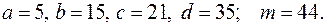
3. Скласти таблицю індексів для модуля 50, взявши за основу первісний корінь 3; з допомогою цієї таблиці розв‘язати конгруенції)  ; б)
; б) 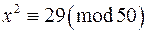 .
.
4. Користуючись таблицями індексів, розв‘язати конгруенції:
а)  ; б)
; б) 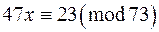 ;
;
в) 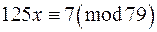 4 г)
4 г)  ;
;
д)  ; е)
; е) 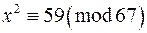 ;
;
є) 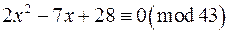 ; ж)
; ж) 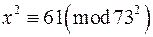 ;
;
5. Скільки розв‘язків мають такі конгруенції:
а) 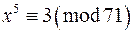 ; б)
; б) 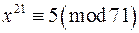 ;
;
в)  ; г)
; г)  ;
;
д) 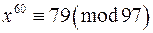 ?
?
6. Розв‘язати двочленні конгруенції:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 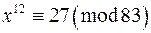 ;
;
д)  ; е)
; е) 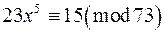 ;
;
є)  ; ж)
; ж) 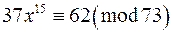 ;
;
з) 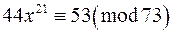 ; к)
; к) 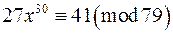 .
.
7. Розв‘язати конгруенції:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е) 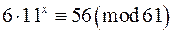 .
.
8. Знайти найменшу натуральне число  , яке задовольняє такі конгруенції:
, яке задовольняє такі конгруенції:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) 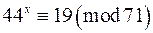 ; е)
; е)  .
.
Задачі рекомендовані для розв‘язування дома
1. Знайти порядок числа  за модулем
за модулем  , якщо:
, якщо:
а) 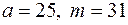 ; б)
; б) 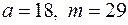 ;
;
в)  ; г)
; г)  .
.
2. Знайти порядки чисел  за модулем
за модулем  , якщо:
, якщо:
а)  ;
;
б)  .
.
3. Знаючи, що 2 є первісним коренем за модулями 101 і 163, розв‘язати показникові конгруенції:
а)  ; б)
; б)  .
.
4. Скласти таблицю індексів для модуля 27, взявши за основу первісний корінь 2; з допомогою цієї таблиці розв‘язати конгруенції)  ; б)
; б)  .
.
5. Визначити число розв‘язків конгруенцій:
а) 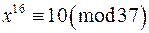 ; б)
; б) 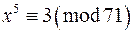 ; в)
; в) 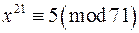 .
.
6. Користуючись таблицями індексів, розв‘язати конгруенції:
а) 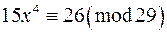 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
7. Розв‘язати конгруенції:
а) 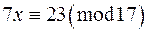 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
є)  ; ж)
; ж)  ;
;
8. Скільки розв‘язків мають такі конгруенції:
а)  ; б)
; б) 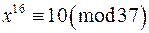 ;
;
в) 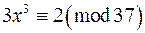 ; г)
; г) 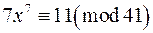 ;
;
д) 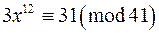 ; е)
; е)  ?
?
9. Розв‘язати двочленні конгруенції:
а) 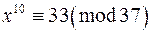 ; б)
; б)  ;
;
в)  ; г)
; г) 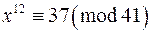 ;
;
д)  ; е)
; е)  ;
;
є) 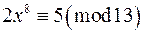 ; ж)
; ж)  ;
;
з)  ; к)
; к)  ;
;
л) 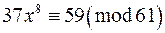 .
.
10. Розв‘язати конгруенції:
а)  ; б)
; б)  ;
;
в) 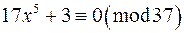 ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
11. Знайти найменшу натуральне число  , яке задовольняє такі конгруенції:
, яке задовольняє такі конгруенції:
а) 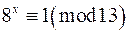 ; б)
; б)  ;
;
в) 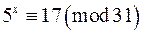 ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
Модуль 3
Практичне заняття 5
Арифметичні застосування теорії конгруенцій
Основні теоретичні відомості:
Теорія конгруенцій має ряд арифметичних застосувань. Основними з них є:
1) виведення ознак подільності;
2)обчислення остач при діленні;
3) перевірка результатів арифметичних дій;
4) визначення довжини періоду при перетворенні звичайного дробу в десятковий.
Нехай в  -й системі числення число
-й системі числення число  має вигляд
має вигляд
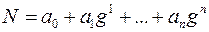
Позначимо через 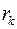 абсолютно найменші лишки числа
абсолютно найменші лишки числа  за модулем
за модулем  , тобто
, тобто  ,
,  і
і 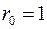 . Тоді
. Тоді  , де
, де  (ознака подільності Паскаля).
(ознака подільності Паскаля).
З конгруенції  випливає, що при діленні на т числа
випливає, що при діленні на т числа  і
і  дають однакові остачі. Зокрема, число
дають однакові остачі. Зокрема, число  ділиться на
ділиться на  тоді і тільки тоді, коли на
тоді і тільки тоді, коли на  ділиться
ділиться  . Покладаючи
. Покладаючи  ,
, 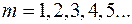 , дістаємо конкретні ознаки подільності. З метою обчислення остач від ділення, крім ознаки Паскаля, використовують також теореми Ейлера і Ферма, властивості індексів тощо.
, дістаємо конкретні ознаки подільності. З метою обчислення остач від ділення, крім ознаки Паскаля, використовують також теореми Ейлера і Ферма, властивості індексів тощо.
Якщо
 (1)
(1)
де  — многочлен від цілих чисел
— многочлен від цілих чисел  з цілими коефіцієнтами, то виконується конгруенція
з цілими коефіцієнтами, то виконується конгруенція
 (2)
(2)
де  —будь-яке натуральне число,
—будь-яке натуральне число,  — остача від ділення
— остача від ділення  на
на  ,
,  . Конгруенція (2) є умова, необхідна для рівності (1), але не достатня. Інакше кажучи, якщо (2) не виконується, то не виконується й (1); якщо (2) виконується, наприклад, для
. Конгруенція (2) є умова, необхідна для рівності (1), але не достатня. Інакше кажучи, якщо (2) не виконується, то не виконується й (1); якщо (2) виконується, наприклад, для 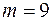 або
або  , то напевно помилки в обчисленнях (1) не виявлено. Так, виконуючи перевірку для
, то напевно помилки в обчисленнях (1) не виявлено. Так, виконуючи перевірку для 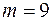 , помилку не виявили, оскільки: 1) не було взято до уваги нуль у доданку або множнику; 2) в результаті цифри записані не в тому порядку; 3) неповні добутки перебувають не на своїх місцях; 4) взагалі, помилка становить число, кратне 9. Під час складних обчислень доцільно робити дві перевірки: одну за модулем 9, а другу — за модулем 11.
, помилку не виявили, оскільки: 1) не було взято до уваги нуль у доданку або множнику; 2) в результаті цифри записані не в тому порядку; 3) неповні добутки перебувають не на своїх місцях; 4) взагалі, помилка становить число, кратне 9. Під час складних обчислень доцільно робити дві перевірки: одну за модулем 9, а другу — за модулем 11.
Нескоротний дріб виду  , де
, де  ,
, 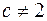 і
і  , у скінчений
, у скінчений
десятковий дріб не перетворюється.
Якщо  — нескоротний дріб і
— нескоротний дріб і 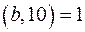 , то цей дріб перетворюється у чистий періодичний десятковий дріб. При цьому число цифр у періоді дорівнює порядку
, то цей дріб перетворюється у чистий періодичний десятковий дріб. При цьому число цифр у періоді дорівнює порядку 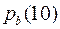 числа 10 за модулем
числа 10 за модулем  .
.
Якщо  — нескоротний дріб і
— нескоротний дріб і  , де
, де  , то цей дріб перетворюється в мішаний періодичний десятковий дріб. При цьому число цифр у періоді дорівнює
, то цей дріб перетворюється в мішаний періодичний десятковий дріб. При цьому число цифр у періоді дорівнює  , де
, де  — більше з чисел
— більше з чисел  і
і  ; число цифр у періоді дорівнює порядку
; число цифр у періоді дорівнює порядку  числа 10 за модулем
числа 10 за модулем  .
.
Задачі рекомендовані для розв‘язання в аудиторії
1. Знайти довжину періоду при перетворенні у десятковий дріб нескоротного звичайного дробу із знаменником: а) 37; б) 59; в) 73.
2. Знайти число цифр до періоду і довжину періоду при перетворенні звичайних дробів у десяткові:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
3. Знайти дві останні цифри числа: а)  ; б)
; б)  , в)
, в)  .
.
4. Знайти остачу від ділення:
а)  на 12; б)
на 12; б)  на 41.
на 41.
5. Знайти три останні цифри числа 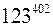 .
.
6. На основі ознаки подільності на 7, 11 і 13 дізнатися, чи діляться числа 769524 і 1353781 на 7, 11 або 13.
7. Перевірити правильність виконання арифметичних дій числами 9 і 11:
а)  ; б)
; б)  .
.
Задачі рекомендовані для розв‘язання дома
1. За допомогою таблиць індексів визначити кількість цифр у періоді розкладу дробів  у нескінченний десятковий дріб.
у нескінченний десятковий дріб.
2. Знайти остачу від ділення: а)  на 21;
на 21;
б)  на 25; в)
на 25; в)  на 57;
на 57;
г) 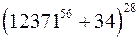 на 243.
на 243.
3. Перевірити правильність результату обчислень числом 9.
а)  ;
;
б)  .
.
4. Перевірити правильність результату обчислень числом 11:
а)  ;
;
б) 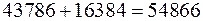 .
.
5. Перевірити правильність виконання арифметичних дій числами 9 і 11:
а)  ; б)
; б)  .
.
Модуль 4
Практичні заняття 1,2
Многочлени над полем  . Дії над многочленами. Подільність
. Дії над многочленами. Подільність
многочленів. Найбільший спільний дільник та
його лінійне зображення. Найменше спільне кратне.
Розклад многочлена на незвідні множники.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 191; Нарушение авторских прав?; Мы поможем в написании вашей работы!