
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні теоретичні відомості
|
|
|
|
Конгруенцію другого степеня виду
 ,
, 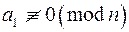 ( 1)
( 1)
завжди можна звести до двочленної конгруенції виду
 (2)
(2)
де  ,
,  ,
,  .
.
Для цього слід обидві частини і модуль конгруенції (1) помножити на  і зробити відповідні перетворення.
і зробити відповідні перетворення.
Якщо конгруенція (2) має хоча б один розв'язок, то  називається квадратичним лишком за модулем
називається квадратичним лишком за модулем  , у противному разі
, у противному разі  називається квадратичним нелишком за модулем
називається квадратичним нелишком за модулем  . При цьому
. При цьому  .
.
Розв'язування конгруенції виду (2) за складеним модулем зводиться до розв'язування таких конгруенцій:
1) 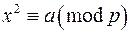 , де
, де  — непарне просте число; (3)
— непарне просте число; (3)
2)  , де
, де  — непарне просте число,
— непарне просте число, 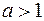 ; (4)
; (4)
3)  , де
, де 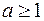 . (5)
. (5)
Найбільш важливим є той випадок, коли модуль є непарним простим числом. При цьому досить обмежитися випадком, коли  , оскільки в противному разі конгруенція (3) має єдиний розв'язок
, оскільки в противному разі конгруенція (3) має єдиний розв'язок 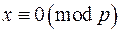 .
.
Отже, надалі розглядатимемо таку конгруенцію:
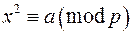 ,
,  , де
, де  — просте непарне число. (6)
— просте непарне число. (6)
Якщо  — квадратичний лишок за модулем
— квадратичний лишок за модулем  , то конгруенція (6) має два розв'язки.
, то конгруенція (6) має два розв'язки.
Для будь-якого простого непарного числа  половина лишків зведеної системи лишків є квадратичними лишками, а половина — квадратичними нелишками.
половина лишків зведеної системи лишків є квадратичними лишками, а половина — квадратичними нелишками.
При простому непарному  число
число  є квадратичним лишком за модулем
є квадратичним лишком за модулем  тоді і тільки тоді, коли
тоді і тільки тоді, коли 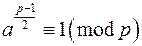 , і квадратичним нелишком тоді і тільки тоді, коли
, і квадратичним нелишком тоді і тільки тоді, коли  (критерій Ейлера).
(критерій Ейлера).
Теорема Ейлера. Добуток двох квадратичних лишків або нелишків є квадратичним лишком за модулем  ; добуток квадратичного лишку на нелишок є квадратичним нелишком.
; добуток квадратичного лишку на нелишок є квадратичним нелишком.
Добуток ряду чисел  дає квадратичний лишок або нелишок залежно від того, парне чи непарне число нелишків буде серед множників.
дає квадратичний лишок або нелишок залежно від того, парне чи непарне число нелишків буде серед множників.
Для ефективного використання критерію Ейлера вводиться так званий символ Лежандра  (читається: «символ Лежандра
(читається: «символ Лежандра  відносно
відносно  », або коротше «
», або коротше « відносно
відносно  », або «
», або « до
до  »),
»),  називається чисельником, а
називається чисельником, а  — знаменником символу Лежандра.
— знаменником символу Лежандра.
Символ Лежандра  визначається для всіх цілих чисел
визначається для всіх цілих чисел  , які не діляться на просте непарне число
, які не діляться на просте непарне число  , рівністю
, рівністю

Критерій Ейлера тоді коротко записується так:
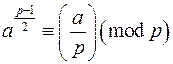 .
.
Основні властивості символу Лежандра:
1°.Якщо 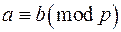 , то
, то  ;
;
2º. 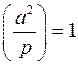 ;
;
3º.  ;
;
4º. 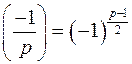 ;
;
5º.  ;
;
6º.  ;
;
7º  ;
;
8º  ;
;
9°. Якщо  і
і  — різні непарні прості числа, то
— різні непарні прості числа, то

(закон взаємності квадратичних лишків).
Узагальненням символу Лежандра є символ Якобі  (читається: «символ Якобі
(читається: «символ Якобі  відносно
відносно  »). Він визначається для будь-яких непарних натуральних чисел
»). Він визначається для будь-яких непарних натуральних чисел  і чисел
і чисел  , взаємно простих з
, взаємно простих з  , рівністю
, рівністю
 ,
,
де  є розкладом
є розкладом  на прості множники (серед них можуть бути і рівні), тобто як добуток символів Лежандра. Для символу Якобі зберігаються властивості 1) — 9) символу Лежандра, проте для символу Якобі йдеться не про непарні прості числа
на прості множники (серед них можуть бути і рівні), тобто як добуток символів Лежандра. Для символу Якобі зберігаються властивості 1) — 9) символу Лежандра, проте для символу Якобі йдеться не про непарні прості числа  , а про непарні натуральні числа
, а про непарні натуральні числа  , для властивості 9) — про взаємно прості непарні числа, відмінні від 1. Тому при визначенні символу Лежандра зручно розглядати його як символ Якобі. При цьому часто немає потреби виділяти з чисельника символу його непарні прості множники.
, для властивості 9) — про взаємно прості непарні числа, відмінні від 1. Тому при визначенні символу Лежандра зручно розглядати його як символ Якобі. При цьому часто немає потреби виділяти з чисельника символу його непарні прості множники.
Конгруенція  , де
, де  — непарне просте число,
— непарне просте число,  ,
,  , має два розв'язки, якщо
, має два розв'язки, якщо  , і не має їх зовсім, якщо
, і не має їх зовсім, якщо
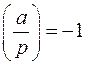 .
.
Для конгруенції  ,
, 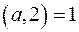 , необхідними умовами існування розв'язків є
, необхідними умовами існування розв'язків є  при
при  ,
,  при
при  .
.
Якщо ці умови виконуються, то існує один розв'язок при  ; два розв'язки при
; два розв'язки при  і чотири розв'язки при
і чотири розв'язки при  .
.
Для конгруенції загального виду  ,
,  ,
, 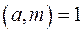 , необхідними і достатніми умовами існування розв'язків є:
, необхідними і достатніми умовами існування розв'язків є:  при
при  ;
;  при
при  .
.
 .
.
Якщо жодну з цих умов не порушено, то число розв'язків дорівнюватиме:
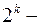 при
при  і
і  ;
;  при
при  ;
; 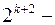 при
при  .
.
Методичні рекомендації до розв‘язування задач
Приклад 1. Скільки розв‘язків має конгруенція  ?
?
Розв‘язання. За властивостями конгруенцій 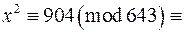
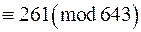 . Знайдемо символ Лежандра
. Знайдемо символ Лежандра 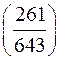 . Оскільки
. Оскільки  , а
, а 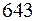 – просте число, то, згідно з властивістю 6,
– просте число, то, згідно з властивістю 6,
 .
.
Обчислимо символ Лежандра  . Оскільки 29 і 643 – різні прості непарні числа, то внаслідок закону взаємності 9) дістаємо
. Оскільки 29 і 643 – різні прості непарні числа, то внаслідок закону взаємності 9) дістаємо
 .
.
За властивістю 1) маємо
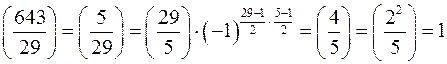 .
.
Отже, дана конгруенція має два розв‘язки.
Зауваження.
1. Слід уважно застосовувати властивість 9), оскільки якщо хоч одне з чисел  чи
чи  є складеним, застосування цієї властивості може призвести до помилок в обчисленні символу Лежандра.
є складеним, застосування цієї властивості може призвести до помилок в обчисленні символу Лежандра.
2. Зауважимо, що коли  – просте непарне число, то символ Лежандра
– просте непарне число, то символ Лежандра  є для конгруенції
є для конгруенції 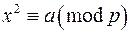 символом Якобі
символом Якобі  і навпаки. Тому для конгруенцій за простим модулем можна не розрізняти символів Лежандра і Якобі, що дає змогу при обчисленні символів Лежандра не розкладати чисельник на прості множники. треба тільки виділяти множники, що дорівнюють
і навпаки. Тому для конгруенцій за простим модулем можна не розрізняти символів Лежандра і Якобі, що дає змогу при обчисленні символів Лежандра не розкладати чисельник на прості множники. треба тільки виділяти множники, що дорівнюють  . Якщо
. Якщо  , то ця конгруенція має два розв‘язки; якщо
, то ця конгруенція має два розв‘язки; якщо  , то конгруенція розв‘язків не має. Для конгруенції
, то конгруенція розв‘язків не має. Для конгруенції  , де
, де  непарне складене число, символ Лежандра не існує, а символ Якобі існує. Проте, якщо символ Якобі
непарне складене число, символ Лежандра не існує, а символ Якобі існує. Проте, якщо символ Якобі  і
і  непарне складене число, то це ще не означає, що конгруенція
непарне складене число, то це ще не означає, що конгруенція  має розв‘язки. Так конгруенція
має розв‘язки. Так конгруенція  розв‘язків не має, а символ Якобі для неї
розв‘язків не має, а символ Якобі для неї  .
.
Приклад 2. Розв‘язати способом проб конгруенцію  .
.
Розв‘язання. Спочатку знаходимо  . Числа 3 і 7 непарні прості. Обчислимо символ Лежандра
. Числа 3 і 7 непарні прості. Обчислимо символ Лежандра  .
.
Отже, дана конгруенція не має розв‘язків.
Приклад 3. Розв‘язати конгруенцію  .
.
Розв‘язання. Для простого модуля старший коефіцієнт взаємно простий з ним. Тоді процес зведення заданої конгруенції до двочленної можна скоротити і навіть залишити модуль незмінним. Так як  , то модуль конгруенції можна не множити на
, то модуль конгруенції можна не множити на  . Помножаючи обидві частини конгруенції на 20 за модулем 43, дістаємо
. Помножаючи обидві частини конгруенції на 20 за модулем 43, дістаємо
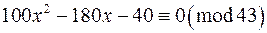 ,
,
або
 ,
,
 .
.
Позначимо  і тоді буде
і тоді буде  . Остання конгруенція має два розв‘язки:
. Остання конгруенція має два розв‘язки: 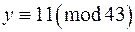 ,
,  .
.
Отже, квадратна конгруенція  має розв‘язки тоді, коли мають розв‘язки конгруенції:
має розв‘язки тоді, коли мають розв‘язки конгруенції:  і
і  . Розв‘язуючи дві останні конгруенції, матимемо:
. Розв‘язуючи дві останні конгруенції, матимемо:
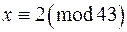 і
і  .
.
Тоді задана конгруенція має розв‘язки  .
.
Приклад 4. Розв‘язати конгруенцію  .
.
Розв‘язання. Конгруенцію  замінюємо системою за простими модулями
замінюємо системою за простими модулями

Спочатку розв‘язуємо конгруенцію 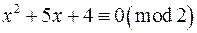 . Застосуємо елементарні перетворення над конгруенціями до виразу зліва
. Застосуємо елементарні перетворення над конгруенціями до виразу зліва  . Конгруенція
. Конгруенція 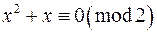 має розв‘язки
має розв‘язки  .
.
Далі розв‘язуємо конгруенцію  . Помножаючи обидві частини конгруенції на 4 за модулем 11, дістаємо
. Помножаючи обидві частини конгруенції на 4 за модулем 11, дістаємо
 ,
,
 ,
,
 .
.
 .
.
Тепер складаємо системи конгруенцій за модулями 2 і 11.
а)  б)
б) 
в) 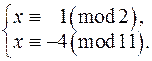 г)
г) 
Розв‘яжемо систему а):  ,
,  ,
,  ,
,  . Отже,
. Отже, 
 .
.
Система конгруенцій б) має розв‘язок:  ,
,  ,
,  ,
,  ,
, 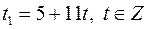 . Отже,
. Отже,  .
.
Розмірковуючи аналогічно, знаходимо розв‘язки систем в)  ,
,  і г)
і г)  ,
,  .
.
Відповідь:  .
.
Приклад 5. Розв‘язати в цілих числах рівняння  .
.
Розв‘язання. Перетворимо дане рівняння і зведемо його до конгруенції.
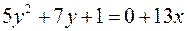 ,
,  . Помножимо обидві частини конгруенції на
. Помножимо обидві частини конгруенції на  .
. 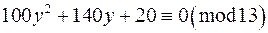 .
.  . Виконаємо підстановку
. Виконаємо підстановку  , матимемо:
, матимемо: 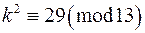 ,
,  ,
,  .
.  .
.
 ,
, 
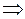
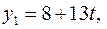
 .
.
Знайдемо  , яке відповідатиме
, яке відповідатиме  ,
,  .
.
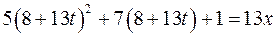 ,
,  ,
,
 ,
,
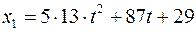 ,
,  .
.
 ,
, 
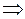

 .
.
Знайдемо  , яке відповідатиме
, яке відповідатиме  ,
,  .
.
 ,
,

 ,
,
 ,
,  .
.
Відповідь:  ,
,  ;
; 
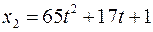 ,
,  .
.
Задачі рекомендовані для розв‘язування в аудиторії
1. Знайти значення символу Лежандра:
а)  ; б)
; б) 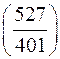 ; в)
; в)  ; г)
; г)  ; д)
; д) 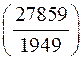 ;
;
е) 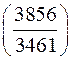 ; є)
; є)  ; ж)
; ж)  ; з)
; з)  ; і)
; і) 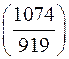 .
.
2. Розв‘язати конгруенції, звівши їх до двочленних:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 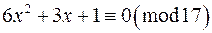 ;
;
д) 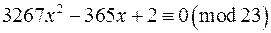 ;
;
е)  ;
;
є)  ;
;
3. Розв‘язати в цілих числах рівняння:
а)  ; б)
; б)  ; в)
; в)  .
.
Задачі рекомендовані для розв‘язування дома
1. Знайти значення символу Лежандра:
а) 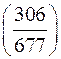 ; б)
; б) 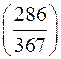 ; в)
; в)  ; г)
; г)  ; д)
; д)  ;
;
е)  ; є)
; є)  ; ж)
; ж) 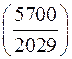 ; з)
; з)  ; і)
; і)  ;
;
к) 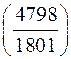 ; л)
; л)  ; м)
; м)  .
.
2. Розв‘язати конгруенції, звівши їх до двочленних:
а)  ; б)
; б)  ;
;
в) 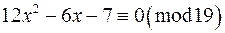 ; г)
; г)  ;
;
д)  ;
;
е)  ;
;
є)  ;
;
ж)  ;
;
з)  .
.
3. Розв‘язати в цілих числах рівняння:
а)  ; б)
; б)  ; в)
; в)  .
.
Модуль 3
Практичне заняття 3
Конгруенції другого степеня за складеним модулем.
Символ Якобі
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 151; Нарушение авторских прав?; Мы поможем в написании вашей работы!