Основні теоретичні відомості 1 страница

Нехай - довільна область цілісності з одиницею і - її підкільце з одиницею.

Елемент називається алгебраїчним над кільцем , якщо в існують такі елементи 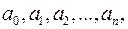які не дорівнюють 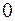, що

Елемент, який не є алгебраїчним над , називається трансцендентним над .

Мінімальне розширення кільця , яке містить трансцендентний над елемент , називається простим трансцендентним розширенням кільця , або кільцем многочленів від однієї змінної над , і позначається через 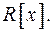Елементи цього кільця називають многочленами від над і позначають символами і так далі. Нуль кільця 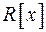називають нульовим многочленом або нуль-многочленом.

Будь-який ненульовий многочлен над кільцем можна єдиним чином подати у вигляді

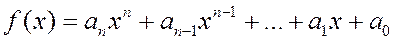, (1)

де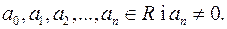

Вираз (1) називають канонічною формою ненульового многочлена . Канонічною формою нуль-многочлена вважатимемо .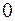

Доданок канонічної форми (1) ненульового многочлена називається 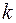-м членом, м коефіцієнтом, 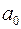називається також вільним членом многочлена . Член -го (найбільшого) степеня називається старшим членом, його коефіцієнт -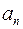

старшим коефіцієнтом, а його степінь – степенем многочлена і позначають

Нуль-многочлену не приписують ніякого степеня.

Два многочлени з кільця 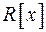дорівнюють один одному тоді і тільки тоді, коли вони мають однакові степені і попарно рівні відповідні коефіцієнти (алгебраїчна рівність многочленів).

Кільце многочленів 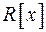є областю цілісності.

Степінь суми двох многочленів (з яких хоча б один є ненульовим) не перевищує більшого з степенів цих многочленів. Степінь добутку двох многочленів (відмінних від нуль-многочлена) дорівнює сумі степенів цих многочленів.

Якщо многочлен з кільця 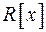має канонічну форму (1) і , то елемент

кільця називають значенням многочлена при і позначають через .

Кожен многочлен з кільця 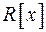визначає відображення таке, що

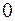Якщо область цілісності має характеристику , то многочлени дорівнюють один одному тоді і тільки тоді, коли рівні функції та , які вони визначають (функціональна рівність многочленів).

Алгебраїчне і функціональне тлумачення многочленів рівносильні над областю цілісності характеристики .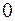

Нехай деяке поле. Многочлен ділиться на (записують 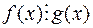), якщо існує многочлен такий, що

Відношення подільності многочленів над полем має такі властивості:

.

Говорять, що многочлен 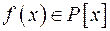ділиться з остачею на многочлен з кільця , якщо в існують такі многочлени що:

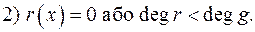
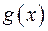При цьому називають діленим, - дільником, 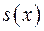- часткою, - остачею.

Довільний многочлен з кільця ділиться з остачею на будь-який ненульовий многочлен 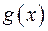з цього кільця, причому частка і остача визначаються однозначно.

Кільце многочленів над довільним полем є кільцем головних ідеалів. Кільце многочленів над полем є евклідовим.

Для знаходження частки і остачі від ділення многочлена

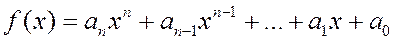
на

над полем застосовують різні методи. Зокрема, метод ділення кутом, метод невизначених коефіцієнтів та за допомогою табличних схем.

Розглянемо одну з можливих табличних схем, яка має іноді переваги перед рештою методів. Нехай 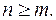Якщо

та

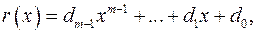
то схема має вигляд (таблиця 1).

Таблиця 1

				…			…
				…
				…
. . .
							…
				…			…

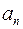
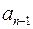
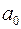
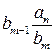
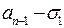
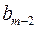
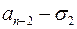
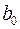
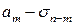
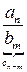
У таблиці є 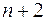стовпці і рядки. Через позначено суму елементів -го стовпця, які стоять між першим та -м рядками. Через позначено суму елементів відповідного стовпця, які стоять між першим і останнім рядками. Таблиця заповнюється так:

1) знаходять 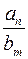і записують його в останній рядок другого стовпця;

2) число множать на коефіцієнти дільника і послідовно записують у другий рядок зліва направо (при цьому кілька останніх клітин можуть бути порожніми);

3) обчислюють різницю і записують її у клітинці на перетині третього рядка і третього стовпця;

4) знаходять число і записують його в третій клітинці останнього рядка;

5) за аналогією з 2) заповнюють третій рядок (при цьому порожньою буде клітинка з другого стовпця).

Цей процес продовжують доти, поки не буде обчислено вільний член 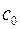частки. Після цього знаходять коефіцієнти остачі як різниці між числом, що стоїть у першому та останніх заповнених рядках відповідного стовпця.

Ділення многочлена на значно спрощується, якщо многочлен є двочленом виду Справді, вона має вигляд таблиці 2. З другого по передостанній рядок цієї таблиці в кожному стовпці міститься не більш як одне число, відмінне від нуля. Наприклад, з другого по 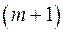-й стовпець – це

Таблиця 2

				…			…			…
. . .
										…
				…			…			…

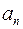
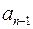
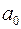
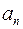
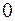
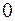
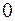
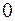
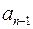
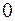
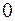
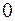
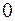
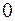
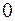
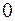
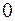
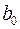
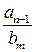
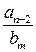
У наступних стовпцях: , тобто добутки вільного члена 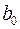дільника на коефіцієнти частки і так далі. Це означає, що в таблиці можна обмежитися тільки трьома рядками і заповнювати її в такій послідовності:

1) спочатку розіб’ємо коефіцієнти многочлена у групи по членів зліва направо (в останній групі може бути менше ніж членів);

2) коефіцієнти записують у першому стовпці в першому і другому рядках;

3) кожен ряд певної групи ділять на старший член дільника і записують у третій рядок під ним; у другому рядку з другої по 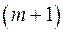-у клітину можна не вписувати чисел;

4) вільний член 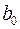послідовно множать на знайдені коефіцієнти частки і вписують у другий рядок, починаючи з -ї клітини;

5) знаходять наступні коефіцієнти частки, і процес продовжують доти, поки не заповнять останню клітину таблиці в третьому рядку.

Якщо двочлен має вигляд то при обчисленні коефіцієнтів частки за наведеною табличною схемою не треба виконувати ділення чисел, тоді ця схема нагадує схему Горнера. При цьому число 1 можна також не писати в лівому верхньому кутку таблиці.

При діленні многочлена на двочлен описану схему можна спростити. Так, якщо усно обчислювати різницю коефіцієнтів і добутків вільного члена - на знайдений коефіцієнт частки 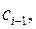то в таблиці стає зайвим другий рядок. Тоді розглядувана таблична схема відрізняється від схеми Горнера тільки тим, що в першому стовпці міститься число замість .

Нехай - деякий многочлен над полем Для будь-якого елемента з поля остача при діленні многочлена на двочлен дорівнює .

Многочлен ділиться на двочлен тоді і тільки тоді, коли остача дорівнює нулю.

Подамо многочлен з кільця у вигляді

де називається розкладом многочлена за степенями . Коефіцієнти розкладу 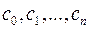можна знайти в результаті послідовного ділення на , потім здобутої першої частки на і так далі.

Нехай і - многочлени над полем . Якщо і діляться на многочлен з кільця , то називають їхнім спільним дільником.

Спільний дільник многочленів і , який ділиться на кожний їхній спільний дільник, називають найбільшим спільним дільником многочленів і і позначають

Дата добавления: 2017-02-01