
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні теоретичні відомості
|
|
|
|
Конгруенція другого степеня за складеним модулем:
 , де
, де  (1)
(1)
досліджується і розв‘язується згідно з загальними вказівками за теоремою:
Якщо  попарно взаємно прості числа, то конгруенція
попарно взаємно прості числа, то конгруенція  (*)
(*)
еквівалентна системі конгруенцій:
 (**)
(**)
При цьому, позначаючи через
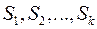
числа розв‘язків окремих конгруенцій (**) за відповідними модулями і через  число розв‘язків конгруенції (*), матимемо:
число розв‘язків конгруенції (*), матимемо:
 .
.
Висновок 1. Якщо хоч одна з конгруенцій системи (**) не має розв‘язків, то й задана конгруенція (*) також не матиме розв‘язків.
Висновок 2. Дослідження і розв‘язування конгруенції
 ,
,
де  канонічний розклад модуля
канонічний розклад модуля  , зводиться до дослідження і розв‘язування конгруенцій:
, зводиться до дослідження і розв‘язування конгруенцій:  . Це випливає з того, що числа
. Це випливає з того, що числа  попарно взаємно прості.
попарно взаємно прості.
За зазначеною теоремою, конгруенція (1) еквівалентна системі конгруенцій
 (2)
(2)
Теорема 2. Конгруенція  має два розв‘язки або не має жодного залежно від того, чи буде число
має два розв‘язки або не має жодного залежно від того, чи буде число  квадратичним лишком або нелишком за модулем
квадратичним лишком або нелишком за модулем  , тобто чи буде відповідно
, тобто чи буде відповідно  або
або  .
.
Теорема 3. 1) Конгруенція  завжди має один розв‘язок при
завжди має один розв‘язок при  ; 2) два розв‘язки – при
; 2) два розв‘язки – при  , і
, і  і жодного при
і жодного при  і
і  ; 3) при
; 3) при  конгруенція
конгруенція  має розв‘язки тільки при
має розв‘язки тільки при  і при цьому чотири різних розв‘язки; два з них неодмінно задовольняють і конгруенцію
і при цьому чотири різних розв‘язки; два з них неодмінно задовольняють і конгруенцію
 . (3)
. (3)
Теорема 4. Конгруенція
 (***)
(***)
має розв‘язок тоді і тільки тоді, коли

 при
при  ,
,
 при
при  .
.
Якщо жодну з цих умов не порушено, то кількість розв‘язків буде
 при
при  ,
,
 при
при  ,
,
 при
при  .
.
Теорема 5. Якщо  задовольняє конгруенцію за простим модулем
задовольняє конгруенцію за простим модулем  :
:
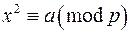 ,
,
де  ,
,
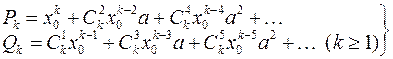 , (4)
, (4)
то 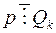 і розв‘язок конгруенції
і розв‘язок конгруенції
 (5)
(5)
має вигляд  , де
, де  розв‘язок конгруенції
розв‘язок конгруенції  .
.
Рівняння Пелля мають вигляд  , де
, де  не є точним квадратом числа.
не є точним квадратом числа.
Якщо розкласти  у неперервний дріб, то дістанемо нескінченний періодичний дріб. Використаємо теорему
у неперервний дріб, то дістанемо нескінченний періодичний дріб. Використаємо теорему 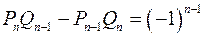 . Рівняння Петля нагадує нам залежність між знаменниками і чисельниками підхідних дробів, виражену вище згаданою теоремою. З правої сторони у теоремі буде стояти одиниця тоді, коли
. Рівняння Петля нагадує нам залежність між знаменниками і чисельниками підхідних дробів, виражену вище згаданою теоремою. З правої сторони у теоремі буде стояти одиниця тоді, коли  буде непарним числом
буде непарним числом  ;
;  . Звідси видно, що рівняння Петля будуть задовольняти чисельники і знаменники підхідних дробів непарного порядку.
. Звідси видно, що рівняння Петля будуть задовольняти чисельники і знаменники підхідних дробів непарного порядку. 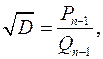
 . На цій основі можна прийняти
. На цій основі можна прийняти  і
і  .
.
Методичні рекомендації до розв‘язування задач
Приклад 1. Розв‘язати конгруенцію 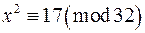 .
.
Розв‘язання. За теоремою 3, конгруенція  при
при  має чотири різні розв‘язки тільки при
має чотири різні розв‘язки тільки при  ; два з них неодмінно задовольняють і конгруенцію
; два з них неодмінно задовольняють і конгруенцію  .
.
При  конгруенція
конгруенція  матиме розв‘язки:
матиме розв‘язки:  і
і 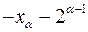 . Отже, спочатку знаходимо розв‘язки конгруенції
. Отже, спочатку знаходимо розв‘язки конгруенції  , а потім методом випробування визначаємо розв‘язки
, а потім методом випробування визначаємо розв‘язки  і
і 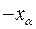 конгруенції за модулем
конгруенції за модулем  . Поступово степінь модуля підвищуємо і приходимо до розв‘язку конгруенції
. Поступово степінь модуля підвищуємо і приходимо до розв‘язку конгруенції  .
.
Методом проб знаходимо один із розв‘язків даної конгруенції:  (
( ). Другим розв‘язком буде:
). Другим розв‘язком буде: 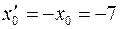 . (
. ( ).
).
Третій і четвертий розв‘язки знаходимо за формулами: 
 ,
,  .
.
Остаточно
 ,
,
або
 .
.
Приклад 2. Розв‘язати конгруенцію  .
.
Розв‘язання. Конгруенція  має розв‘язок
має розв‘язок  .
.
Взявши  ,
,  , обчислимо:
, обчислимо:
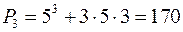 ,
,  .
.
Розв‘язуючи конгруенцію  , знаходимо
, знаходимо  , тому
, тому  .
.
Відповідь:  .
.
Приклад 3. Визначити, чи має розв‘язки конгруенція
 ,
,
і якщо має, то скільки.
Розв‘язання. Знаходимо канонічний розклад модуля; маємо:  ; далі
; далі
 [теорема 3].
[теорема 3].  ;
;  .
.
Отже, ця конгруенція має  розв‘язків, бо тут
розв‘язків, бо тут  [теорема 4].
[теорема 4].
Приклад 4. Розв‘язати рівняння  в цілих числах.
в цілих числах.
Розв‘язання. Розкладемо у ланцюговий дріб число  і складемо таблицю для відшукання
і складемо таблицю для відшукання  .
.
 .
.
 .
.
Чисельники і знаменники підхідних дробів непарного порядку набувають значень:  ,
,  , де
, де 
Отже, рівняння  має розв‘язки:
має розв‘язки:
 .
.
Задачі рекомендовані для розв‘язування в аудиторії
1. Звести такі квадратичні конгруенції до двочленних:
а)  ; б)
; б)  ;
;
в)  .
.
2. Показати, що конгруенція  має два розв‘язки.
має два розв‘язки.
3. Розв‘язати конгруенції:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 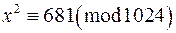 ;
;
д)  .
.
Задачі рекомендовані для розв‘язування дома
1. Показати, що конгруенції мають розв‘язки:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
2. Розв‘язати конгруенції:
а)  ; б)
; б)  ;
;
в) 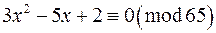 ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
є)  ; ж)
; ж)  .
.
Модуль 3
Практичне заняття 4
Індекси за простим модулем.
Двочленні конгруенції за простим модулем.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 498; Нарушение авторских прав?; Мы поможем в написании вашей работы!