Алгебраические дополнения и миноры

Решение.

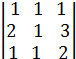= . Умножим 1-ю строку на (-1) и прибавим к третьей получим

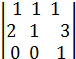= = 1 + 0 + 0 – 0 – 0 – 2 = -1. Для проверки свойства 8, вычислим исходный определитель по правилу треугольника = 2 + 3 + 2 – 1 -3 -4 = -1.

Как видно из результатов вычислений, свойство 8 выполняется.

Прежде чем сформулировать свойство 9, рассмотрим некоторые новые математические понятия.

Для наглядности снова раскроем определитель 3-го порядка по правилу треуголь-ника

= = + + - - -

= ( - ) + ( - ) + ( - ).

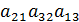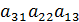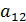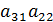Выражения в скобках называются алгебраическими дополнениями элементов первой строки и обозначаются:

= - ; = ; = -

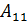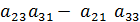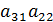
Аналогично, можно сгруппировать члены относительно элементов любой строки или любого столбца и получить алгебраические дополнения элементов этих строк или столбцов. Таким образом, значения определителя равно произведе-

ниям элементов какой – либо строки или столбца на их алгебраические допол-

нения. 6

9). Определитель равен сумме произведений элементов какой-либо строки или столбца на соответствующие алгебраические дополнения элементов этих строк или столбцов.

Находить алгебраические дополнения таким образом нерационально, есть дру-

гой способ.

Определение. Минором данного элемента определителя n-го порядка называ- ется определитель (n – 1) –го порядка, получаемый из данного определителя путём вычёркивания той строки и того столбца на пересечении которых стоит данный элемент.

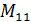Минор элемента = = = , а минор элемента 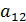= = = - . Сравним эти миноры с алгебраическими дополнениями этих же элементов. Приходим к выводу, что миноры и алгебраические дополнения с точностью до знака совпадают, аналитически это выражается формулой

Замечание. Сумма произведений элементов какой –либо строки или столбца на алгебраические дополнения элементов другой строки или столбца равна 0.

Вывод: девятое свойство является способом вычисления определителей порядка выше третьего.

Пример. Применяя свойства, вычислить определитель 4-го порядка.

D =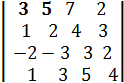

Решение. Произведём следующие действия: 1) из элементов 1-й строки вычтем утроенные элементы 2-й строки; 2) к элементам 3-й строки прибавим удвоенные элементы 2-й строки; 3) из элементов 4-й строки вычтем элементы 2-й строки. Тогда исходный определитель преобразуется к виду

D = .

Разложим этот определитель по элементам 1-го столбца:

D = - .

Прибавляя к элементам 1-й строки элементы 3-й строки и вычитая из элементов 2-й строки элементы 3-й строки, получим

D = - .

Разложим определитель по элементам 1-го столбца:

D = - = 70.

Определение. Определитель, у которого элементы, стоящие ниже или выше диагонали все нули, имеет диагональный вид.

Дата добавления: 2017-02-01