Лекция 4. Общая теория решения систем линейных уравнений.

Рассмотрим систему m линейных уравнений с n неизвестными

Определение. Система (1) называется совместной, если она имеет решение и несовместной, если она не имеет решений.

Определение. Совместная система линейных уравнений называется определённой, если она имеет единственное решение и неопределённой, если она имеет бесчисленное множество решений.

Определение. Две совместные системы уравнений называются равносильными, если каждое решение первой системы является решением второй и обратно.

Теорема Кронекера - Капелли. Кронекер (1823-1891)- немецкий математик. Капелли (1855-1910)-итальянский математик.

Для того, чтобы система линейных уравнений (1) была совместна, необходимо и достаточно, чтобы ранг матрицы системы

был равен рангу её расширенной матрицы

B = , полученную путём добавления к основной матрице А столбца из свободных членов системы.

1). Если r(A) = r(B) = n – числу неизвестных, то система (1) имеет единственное решение.

2). Если же r(A) = r(B) < n, то система (1) имеет бесчисленное множество решений, зависящих от (n – r) параметров (свободных неизвестных).

МЕТОД ГАУССА (Метод последовательных исключений)

Этот метод продемонстрируем на примере, так как он запрограммирован на электронных машинах и хорошо там просчитывается.

Пример. Решить систему уравнений методом Гаусса.

Установим совместность системы, найдём ранг матрицы, составленной из коэффициентов при неизвестных

det A = =-9+1+30+6-6- 0, значит ранг матрицы А равен 3. Составим расширенную матрицу

В = , так как в ней содержится det A , то rang B также равен 3. Делаем вывод: согласно теореме Кронекера-Капелли r(A)=r(B)=3-числу неизвестных, поэтому система совместна и имеет единственное решение.

Решение. Из 1-го уравнения выражаем и подставляем во 2-е и 3-е Из 2-го уравнения выражаем и подставляем в 3-е.

Теперь обратным ходом из 3-го выражаем 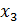и подставляем во 2-е уравнение, из 2-го выражаем и подставляем 1-е, окончательно получаем: 3; = 2; 1.

Ответ: ; ; 3.

Дата добавления: 2017-02-01