Лекция. 3 Матричная запись и матричное решение систем уравнений 1-го порядка. Ранг матрицы.

Собственные числа и собственные векторы матрицы

Определение. Характеристическим уравнением матрицы А =

называется уравнение

Корни этого уравнения называются характеристическими числами матрицы.

Определение. Система уравнений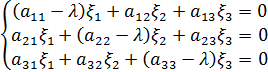

в которой имеет одно из значений (и определитель которой в силу этого равен 0) определяет тройку чисел (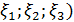, соответствующую данному характеристическому числу, эта совокупность трёх чисел определяет вектор

, называемый собственным вектором матрицы

Пример. Дана матрица , найти её характеристические числа и собственные векторы.

Решение. Составляем характеристическое уравнение = 0 .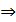

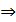
1). подставляем в систему эта система имеет бесчисленное множество решений, полагаем , тогда и собственный вектор .

Аналогично.

2). , , .

Пусть дана система алгебраических уравнений

Коротко эту систему можно записать в тензорном виде:

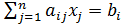, i = 1 m. (2)

Обозначим:

A = ; X = ; B = ,

тогда

A∙X = ∙ = = . (3)

Такая запись (3) системы называется матричной формой.

A X = B операторная форма (4)

Обе части равенства (4) умножим слева на обратную матрицу

A X = B, получим E X = X, но E X = X, поэтому

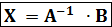-матричное решение системы (1).

Пример. Матричным методом решить систему:

Решение. Решение будем находить в виде X = 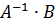, для этого найдём обратную матрицу для матрицы А, составленную из коэффициентов при неизвестных

А , X = , B = .

Матрица найдена в предыдущем примере:

=

X = = =

Ответ: .

Дата добавления: 2017-02-01