
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условие компланарности векторов
|
|
|
|
Координатная форма смешанного произведения
Cвойства смешанного произведения
Cмешанное произведение векторов
Определение. Смешанным произведением 3-х векторов  ,
,  называется скалярное произведение вектора [
называется скалярное произведение вектора [  на вектор
на вектор  , ([
, ([  .
.
Обозначается: ( или (
или (
1). ([  = (
= ( ;
;
2). ( = - (
= - (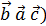 = (
= ( = - (
= - ( = +(
= +(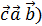 ;
;
3). (α  ,
,  .
.
Доказательство этих свойств следует из свойств определителей, что мы и увидим в дальнейшем.
Геометрический смысл смешанного произведения ( 

 = [
= [ 

 S. По определению ([
S. По определению ([  =
=
 h =
h =  = S
= S 
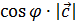 =
=
 ={h =
={h = 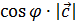 } = S
} = S  = V.
= V.
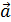 Угол
Угол  может быть <
может быть <  и >
и >  , то есть
, то есть  < 0 или
< 0 или  >0, поэтому
>0, поэтому 
Вывод: Смешанное произведение векторов с точностью до знака равно объёму параллелепипеда, построенного на векторах сомножителях.
Пусть вектор 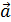 = { X1, Y1 Z1 }; вектор
= { X1, Y1 Z1 }; вектор  = { X2,Y2 ,Z2 }; вектор
= { X2,Y2 ,Z2 }; вектор  = {X3 ,Y3 , Z3 }.
= {X3 ,Y3 , Z3 }.
[ 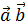 ] =
] =  =
= 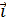
 -
- 
 +
+  . Известно, что скалярное произведение - это произведение одноимённых координат, поэтому
. Известно, что скалярное произведение - это произведение одноимённых координат, поэтому
( X3 -
X3 -  Y3 +
Y3 + 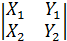 Z3 , c другой стороны - это разложение определителя третьего порядка по элементам третьей строки.
Z3 , c другой стороны - это разложение определителя третьего порядка по элементам третьей строки.
 = (
= (  (
( 
Используя формулу ( , можно доказать все свойства (1,2,3) смешанного произведения.
, можно доказать все свойства (1,2,3) смешанного произведения.
Пример. Вычислить объём пирамиды с вершинами в точках: О (0,0,0); А(5,2,0); В (2, 5, 0); С (1,2,4).
Решение. Объём пирамиды равен  объёма параллелепипеда, то есть = Vпир. =
объёма параллелепипеда, то есть = Vпир. =  Vпар. =
Vпар. =  ,
,  =
=  =
=  ( 100 -16) = 84 куб.ед.
( 100 -16) = 84 куб.ед.
Ответ: Vпир. = 84 куб. ед.
Теорема. Необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения.
Доказательство необходимости. Пусть  компланарны, значит построить параллелепипед на них нельзя, то есть объём равен нулю V=0, а это значит и
компланарны, значит построить параллелепипед на них нельзя, то есть объём равен нулю V=0, а это значит и  =0 ч.т.д.
=0 ч.т.д.
Доказательство достаточности. Пусть (  = 0 это значит, что V=0 и векторы
= 0 это значит, что V=0 и векторы  лежат в одной плоскости, то есть компланарны ч.т.д.
лежат в одной плоскости, то есть компланарны ч.т.д.
Вывод: Условием компланарности векторов является равенство нулю их смешанного произведения  = 0
= 0
Пример. Проверить лежат ли четыре точки в одной плоскости. А (2,-1,1); В(5,5,4); С(3,2,-1); Д(4,1,3).
Решение. Надо проверить лежат ли 3 вектора  в одной плоскости, для этого найдём координаты этих векторов
в одной плоскости, для этого найдём координаты этих векторов  {3,6,3};
{3,6,3};  { 1,3,-2};
{ 1,3,-2}; 
( 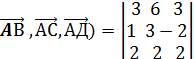 = 18 -24 +6 -18-12+ 12= 18
= 18 -24 +6 -18-12+ 12= 18  . Вывод. Эти точки
. Вывод. Эти точки
не лежат в одной плоскости.
Определение. Двойным векторным произведением векторов  называется векторное произведение [
называется векторное произведение [ 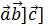 или [
или [  .
.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 86; Нарушение авторских прав?; Мы поможем в написании вашей работы!