Аналитическая геометрия

Задачи

Задача 1. Какому условию должны удовлетворять векторы , чтобы вектор 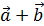делил пополам угол между векторами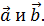

Задача 2. Точка 0 является центром тяжести треугольника АВС. Доказать, что

.

Задача 3. Найти сумму и разность векторов 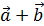и , если ;

Задача 4. Дан вектор ; Угол между векторами равен 60⁰. Найти =?

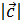Задача 5. Даны 3 вектора , Определить разложение вектора по базису .

Лекция 9. Основные понятия. Различные виды уравнения прямой на плоскости.

Аналитическая геометрия имеет своей задачей изучение свойств геометрических объектов при помощи аналитического метода. В основе этого метода лежит метод координат, впервые применённый Декартом (великий французский математик и философ 1596-1650). Начальные (основные) понятия аналитической геометрии – точка, прямая линия, плоскость, поверхность.

Понятие об уравнении линии.

Определение. Линия L – это геометрическое множество точек, координаты которых удовлетворяют уравнению

Ф(x,y) = 0 или (1)

F(x,y) = 0.

Для более удобного построения линий L, часто вводят вспомогательную переменную или параметр t.

(2)

Исключив из (2) параметр t, перейдём к (1).

Пример. Получить уравнение окружности с центром в начале координат и радиусом r.

Решение. Сделаем рисунок.

y

t

r Из рисунка видно

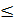oo t x 0 t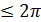

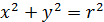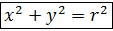
Эти уравнения (3) и есть параметрические уравнения окружности. Обе части уравнений (3) возведём в квадрат и сложим . уравнение окружности с центром в точке О(0,0) и радиусом r.

Можно вывести уравнение циклоиды – это линия, которую описывает точка М на окружности, если окружность без скольжения движется по прямой.

y

0 x

Определение. Линия называется алгебраической, если в некоторой декартовой системе координат она определяется уравнением Ф(x,y)=0, где Ф(x,y) – алгебраический полином – многочлен.

Определение. Алгебраическая линия называется порядка n, если Ф(x,y) многочлен n-ой степени.

Ф(x,y)= Аx+By+C=0 1-ой степени

Ф(x,y)= A 2-ой степени

Ф(x,y)= A 3-й степени.

Определение. Всякая неалгебраическая линия называется трансцендентной.

УРАВНЕНИЕ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ

Определение. Уравнение Ф(x,y,z)=0 называется уравнением поверхности S

относительно д.с.к., если этому уравнению удовлетворяют координаты x,y,z, любой точки, лежащей на поверхности S.

c

Например: z...M

x y М(x,y,z); С(a,b,c) МС =r= или

- это уравнение сферической поверхности

Определение. Линию в рассматривают, как пересечение 2-х поверхностей.

РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ

Общее уравнение прямой.

_{y N}

_M .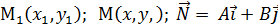

_M1 = .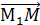

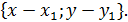
_{0 x} ( ∙ )=0 или

A(x- , раскроем скобки

Ax + By +(-A , обозначим

(-Аx-By)=C,получим 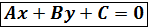- общее уравнение прямой.

Неполные уравнения прямой.

1). С=0, Ax+By=0 - прямая проходит через начало координат.

2). B=0, Ax+C =0 - прямая параллельна оси оy.

3). A=0, By+C =0 - прямая параллельна оси ox.

4). B=C=0, Ax=0, x=0 - ось oy.

5). А=С=0, Вy =0, y=0 - ось оx.

Дата добавления: 2017-02-01