Физический смысл скалярного произведения

ЛЕКЦИЯ 7. Скалярное произведение векторов. Векторное произведение.

Деление отрезка в данном отношении

Условия коллинеарности двух векторов

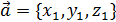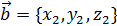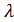
Пусть вектор коллинеарен вектору , тогда по теореме () имеем = , = , из этих равенств находим , то есть 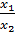; ; = 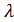, приравниваем левые части этих равенств 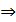условие коллинеарности векторов.

Правило. Если векторы коллинеарны, то их координаты пропорциональны.

Определение. Единичный вектор, направленный по вектору 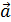, называется его ортом и обозначается

Пример. Найти орт вектора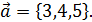

Решение. Найдём модуль вектора , тогда орт вектора запишется = { }.

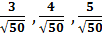Определение. Разделить отрезок 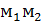в данном отношении это значит найти на данном отрезке такую точку М, что имеет место равенство или М₁М .

Пусть даны точк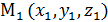и и 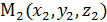, найдём координаты точки М (x, y, z), делящей отрезок 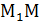₂ в отношении .

Z М₁ М = { x - x₁, y – y₁, z – z₁ };

M₂ = { x₂ – x, y₂ – y, z₂ – z }.

x o y по теореме () в координатах

x – x₁ = (x₂ – x) x (1+ )= x₂ +x₁ x = y – y₁ = (y₂ – y) y (1+ ) = y₂ + y₁ y =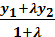

z – z₁ = (z₂ – z) z (1+ ) = z₂ + z₁ z =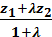

Если точка М середина отрезка, то М₁ М = М М₂ и = 1, тогда

X_cp. = , Y_cp. = 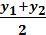, Z_cp. = .

Если < 0, то точка М лежит вне отрезка М₁ М₂.

Определение. Скалярным произведением векторов 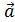и называется число, равное произведению модулей этих векторов на косинус угла между ними.

Обозначается ( =

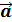
Из физики известно, что работа силы по перемещению, находится по формуле А = F S F

S

Если вектор силы, а вектор перемещения, то работа А = = = (, то есть работа равна скалярному произведению векторов силы и пути

Дата добавления: 2017-02-01