ЛЕКЦИЯ 8. Выражение векторного произведения через координаты перемножаемых векторов . Смешанное произведение.

Физический смысл векторного произведения

1). Рассмотрим физическую задачу.

Пусть твёрдое тело вращается с угловой скоростью вокруг неподвижной оси.

М – произвольная точка, - линейная скорость,

z направленная по касательной к окружности,

описываемой точкой М.

ddD 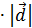, ⊥ оси oz, из треугольника

OO₁M , тогда так как ⊥ и 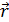, а поворот от к 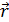против ча

совой стрелки, то линейную скорость можно рас-

y сматривать как векторное произведение, то есть

x Вывод: векторное произведение угловой скорос - ти на радиус – вектор произвольной точки вращающегося тела есть линейная скорость.

M M ]

2). Можно показать, что вращающий момент силы , приложенной к точке В тела есть векторное произведение вектора –плеча на вектор-силы.

A

AAA

B

Пусть вектор и вектор найдём векторное произведение этих векторов

[ , ] =

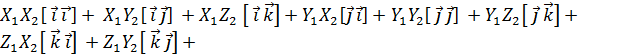
= { = = =0, } = = = { раскроем этот определитель по элементам первой строки, получим } = [

ВЫВОД. Векторное произведение равно определителю третьего порядка, элементами которого являются базисные векторы 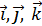(первая строка), координаты перемножаемых векторов (вторая строка); (третья строка ).

Замечание. Векторное произведение базисных векторов 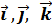находят по правилу правых и левых троек

= =

=- =

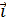
0 = - = -

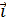
Пример 1. Сила = {1, 0, 4 } приложена к точке С (1, 2, 3). Найти момент этой силы относительно точки D (1, 4, 5).

Решение. ,координаты вектора = { 0, -2, -2}.

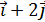= -8 + 2 .

Ответ: { -8,2,2}.

Пример 2. Вычислить площадь параллелограмма, построенного на векторах 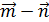, где ; угол между векторами и равен 60⁰.

Решение. S = 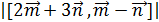= = 5 ⁰ = 5 3 2 =15 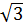кв.ед. Ответ: S = 15

Пример 3. Вычислить площадь треугольника, вершины которого находятся в точках А (2,3,1); В (5, 6, 3); С (7, 1, 10).

Решение. S = S = 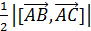. Найдём координаты векторов , для

этого из координат конца вычтем координаты начала, получим {3,3,2}; 30

{5,-2,9}. S = = = = = ед. Ответ: S = ед.

Дата добавления: 2017-02-01