Задачи на движение по замкнутой трассе

Задачи на движение по прямой вдогонку

Задачи на движениевдогонку для слабых обучающихся решаются аналогично.

Прототип задания B13 (№ 99595). Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?

«Сплетничаем»: Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Составляем таблицу и анализируем условие по данной фразе. 300 м = 0,3 км. И продолжаем заполнение: «Через сколько минут расстояние между пешеходами станет равным 300 метрам?»

	S, км	v,	t, ч
I	t(х+1,5) -	х+1,5,	t, t>0?
II	- t х =	х, х>0	t
	0,3

Получим уравнение t(х+1,5) - t х = 0,3, 1,5 t = 0,3, t= 0,2. Ответили ли мы на вопрос: «Через сколько минут»? 0,2 ч = 0,2 60 мин = 12 мин.

Ответ: 12.

Для сильных учащихся необходимо напомнить, что если расстояние между телами S, они движутся по прямой со скоростями v₁ и v₂ соответственно (v₁ > v₂)так, что первое тело следует за вторым, то время t, через которое первое тело догонит второе, находится по формуле . Поэтому задача решается арифметически: t= , t= 0,2 ч, т.е. 12 мин.

Как правило, вызывают затруднения задачи на движения по замкнутой трассе( по окружности). Решаются они почти так же, как и обычные задачи на движение. В них тоже применяется формула . Но есть одна хитрость.

Прототип задания B13 (№ 99599) Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

Во-первых, переведем минуты в часы, поскольку скорость надо найти в км/ч. Скорости участников обозначим за х и у. В первый раз мотоциклист обогнал велосипедиста через 10 минут, то есть через часа после старта. До этого момента велосипедист был в пути 40 минут, то есть часа. Запишем эти данные в таблицу:

I встреча	S, км	v,	t, ч
велосипедист	х =	х, х>0
мотоциклист	= у		у, у>0?

Имеем у = х, т.е. = 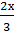, у = 4 х.

Затем мотоциклист второй раз обогнал велосипедиста. Произошло это через 30 минут, то есть через часа после первого обгона.

Заполним вторую таблицу.

II встреча	S, км	v,	t, ч
велосипедист	х =	х, х>0
мотоциклист			4 х?

А какие же расстояния они проехали? Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна 30 км. Получим второе уравнение: 2 х - = 30, 1,5 х = 30, х, 4 х= 80.

Ответ: 80.

Прототип задания B13 (№ 99600). Часы со стрелками показывают

8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Это, пожалуй, самая сложная задача В13. За один час минутная стрелка проходит один круг, а часовая часть круга. Пусть их скорости равны

1 круг/ ч и круг/ч. Старт — в 8:00. Найдем время, за которое минутная стрелка в первый раз догонит часовую.

I встреча	S, круг	v,	t, ч
минутная
часовая
минутная	1 t -		t
часовая	- t =		t
разница в пути	=

Минутная стрелка проходит за 1 час 1 круг, а часовая меньше на круга, поэтому уравнение будет таким: t - = . Решив его, получим, что t = часа. Итак, в первый раз стрелки поравняются через часа.

Пусть во второй раз они поравняются через время t₁, разница в пройденном пути составит 1 круг.

II встреча	S, круг	v,	t, ч
минутная	1 t1 -		t1
часовая	- t1 =		t1
разница в пути	=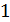

Запишем уравнение: t₁ - = 1, t₁ = . Итак, через часа стрелки поравняются во второй раз, еще через часа — в третий, и еще через часа — в четвертый. Значит, если старт был в 8.00, то в четвертый раз стрелки поравняются через + 3 = 4 часа.

Дата добавления: 2017-02-01