Задачи на движение по реке

Задачи на вычисление средней скорости

В Открытом банке данных встречаются задачи на вычисление средней скорости. [2, 3, 11, 13]

Прототип задания B13 (№ 99606). Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Обучающиеся должны знать, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле: v_средмн = . Если участков пути было два, то v_средмн =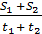

	S, км	v,	t, ч
I часть пути	50 2
II часть пути	100 1
III часть пути	75 2
Средние значения	50 + 100 + 150		2+1+2

Итак, v_средмн = , v_средмн = 60.

Ответ: 60.

Следующий тип задач — когда что-нибудь плавает по реке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучего судна и скорости течения. Собственной скоростью называется скорость в неподвижной воде. Течение помогает, по течению плыть — быстрее. Скорость при движении по течению равна сумме собственной скорости судна и скорости течения. А если двигаться против течения? Течение будет мешать, относить назад. Теперь скорость течения будет вычитаться из собственной скорости судна. Скорость плота считается равной скорости течения реки. [14]

Прототип задания B13 (№ 99602). Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.

«Сплетничаем»: Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления.

Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Пусть скорость лодки в неподвижной воде х .

	S, км	v,	t, ч
против течения		х - 1, х>1
по течению		х + 1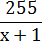

К последнему столбцу надо применить последнее данное: «вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше».

	S, км	v,	t, ч
против течения		х - 1, х>1	-
по течению		х + 1	- =
разница во времени			= 2

Получаем уравнение: - = 2. ,

= 2, , х₁ =16 и х₂ = - 16 (не удовлетворяет ограничению х>1).

Прототип задания B13 (№ 26588). Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.

	S, км	v,	t, ч
по течению		15 + х	+
стоянка			+ 10 +
против течения		15 - x, 0 <х< 15	+ =
затрачено времени			= 40

Получаем уравнение: + + 10 = 40, решая, получим х² = 25, т.е. х₁ = 5 и х₂ = - 5 (не удовлетворяет ограничению 0 <х< 15).

Ответ: 5.

Прототип задания B13 (№ 26587). Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт А в 16:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.

Пусть скорость течения равна х км/ч. Сколько времени баржа плыла? Ясно, что надо из 16 вычесть 10. 1 час 20 минут = 1 часа = ч.

	S, км	v,	t, ч
по течению		7 + x	+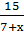
стоянка			+ +
против течения		7 - х, 0 <х< 7	+ =
затрачено времени			= 6

Решив задачу, получаем х₁ =2 и х₂ = - 2 (не удовлетворяет ограничению 0 <х< 7).

Ответ: 2.

Дата добавления: 2017-02-01