
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи на растворы, смеси и сплавы
|
|
|
|
Задачи на проценты
Основными типами задач на проценты являются следующие:
1) задачи на растворы, смеси и сплавы,
2) задача «о продуктах» (о процентном содержании какого – либо вещества),
3) задачи на формулу сложных процентов.
Тип задач на растворы, смеси, сплавы встречаются не только в математике, но и в химии. Самый простой способ их решения – это при решении задач короткую запись задачи можно сделать с помощью таблицы. Таблица является универсальным средством и позволяет решать большое количество идейно близких задач с использованием аналогий.
Прототип задания B13 (№ 99571). В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
После первого прочтения задачи строим таблицу.
| Всё количество, л (100%) | Часть количества (чистое вещество), л | % содержание чистого вещества | |
| I (вещество) | |||
| II (вода) | |||
| I + II (раствор) |
Разбиваем текст на логические части и анализируем. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества. I-го вещества 5 л, % содержание – 12%
| Всё количество, л (100%) | Часть количества (чистое вещество), л | % содержание чистого вещества | |
| I (вещество) | |||
| II (вода) | |||
| I + II (раствор) |
Заполнены две ячейки строки, необходимо заполнить последнюю ячейку. Задачи на пропорции даже слабые учащиеся решают хорошо, поэтому, не запоминая формул, составляем пропорцию:
5 л – 100%  , х =
, х = 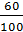 . Лучше пока не сокращать дробь.
. Лучше пока не сокращать дробь.
х л – 12% Продолжаем заполнение таблицы.
| Всё количество, л (100%) | Часть количества (чистое вещество), л | % содержание чистого вещества | |
| I (вещество) | 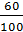
| ||
| II (вода) | |||
| I + II (раствор) |
Фраза «добавили 7 литров воды» говорит о том, что она имеет 0% концентрации, т.е. в ней не содержится чистого вещества. Значит, в строке II (вода) кроме первой ячейки (7 л), следует поставить «0». Ответ на вопрос задачи «Сколько процентов составляет концентрация получившегося раствора?» поможет найти слово «добавили», т.е. речь идет о сумме I + II (раствор). Заполняем таблицу.
| Всё количество, л (100%) | Часть количества (чистое вещество), л | % содержание чистого вещества | ||
| I (вещество) | 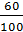
| |||
| II (вода) | ||||
| I + II (раствор) | 5+7=12 | 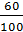 + 0 = + 0 = 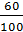
|
|
Важно постоянно напоминать обучающимся, что в смесях, растворах и сплавах % содержание не является средним арифметическим (аналогия со средней скоростью, определением времени при общей работе и т.п.). Опять используем умение решать задачи на пропорции.
12 л – 100%  , у =
, у =  , у = 5.
, у = 5.
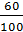 л – у %
л – у %
Ответ: 5.
Прототип задания B13 (№ 99572). Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
«Сплетничаем»: Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Вспомним, что если объем работы не важен в задаче и нет никаких данных, позволяющих его найти - работа принимается за единицу. Аналогично, если объем раствор не важен в задаче и нет никаких данных, позволяющих его найти – объем раствора принимается за единицу х. Пусть масса первого раствора равна 1. Масса второго – тоже 1.
| Всё количество, (100%) | Часть количества (чистое вещество) | % содержание чистого вещества | ||
| I | 1 + |  + +
| ||
| II | + 1 = | +  = =
| ||
| I + II | = 2 | = 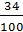
|
|
Составляем пропорцию.
2– 100% х =  , х = 17.
, х = 17.
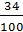 – х % Ответ: 17.
– х % Ответ: 17.
Прототип задания B13 (№ 99575). Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
«Сплетничаем»: Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Пусть масса первого сплава равна х, т.к. I + II 200 кг, тогда масса II сплава (200 – х) кг.
| Всё количество, кг (100%) | Часть количества (никель), кг | % содержание никеля | |
| I | х |  х + х +
| |
| II | 200 – х | + 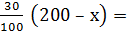
| |
| I + II | = 50 |
 х +
х + 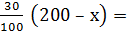 50,
50,  х –
х –  х+ 60=50, 0,2 х = 10, х = 50.
х+ 60=50, 0,2 х = 10, х = 50.
В таблице нет знака вопроса, значит, ответа на вопрос задачи мы не получили. Читаем вопрос: «На сколько килограммов масса первого сплава меньше массы второго?»
1) 200 – 50 = 150 (кг) – масса второго сплава.
2) 150 – 50 = 100 (кг).
Ответ: 100.
Прототип задания B13 (№ 99577). Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
| Всё количество, кг (100%) | Часть количества (чистое вещество), кг | % содержание чистого вещества | ||
| I (кислота) |
|  х + х +
| ||
| II (кислота) | у | + 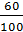 у + у +
| ||
| III (вода) | + 0 = | |||
| I + II + III | х + у + 10 | = 
| ||
| I (кислота) |
|  х + х +
| ||
| II (кислота) | у | + 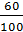 у + у +
| ||
| III (кислота) | + 5 | |||
| I + II + III | х + у + 10 | = 
|

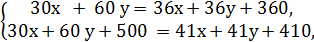
5 х + 5 у = 450, х + у = 90, у = 90 – х. Из первого уравнения системы 4 у – х = 60,
360 – 4 х – х = 60, х = 60.
Ответ: 60.
3.2. Задачи «о продуктах»
Если встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог – на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. [5, 6, 7, 11 – 15]
Прототип задания B13 (№ 99574). Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
В винограде содержалось 90% воды, значит, «сухого вещества» было 10%. В изюме 5% воды и 95% «сухого вещества». «Сухое вещество» остается неизменным.
| Всё количество, кг (100%) | Часть количества (сухое вещество), кг | % содержание сухого вещества | ||
| виноград |
|  х= х=
| 100 – 90 = 10 | |
| изюм | = 
| 100 –5 = 95 |
 х =
х =  , х= 190.
, х= 190.
Ответ: 190.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 90; Нарушение авторских прав?; Мы поможем в написании вашей работы!