| № п/п
| Раздел
(название)
| Название темы, литература
| Содержание
(не более 2-3 строк)
| Коды формируемых компетенций
|
|
| Раздел 1 Случайные события
| Тема 1.1 Предмет теории вероятностей. Классическое определение вероятности Аксиомы вероятностного пространства. Теорема сложения вероятностей
| Основные понятия комбинаторики: правила умножения и сложения; перестановки и сочетания. При классическом определении вероятность события определяется равенством Р(А)= 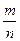 , где m- число элементарных исходов испытания, благоприятствующих появлению события А; n- общее число возможных элементарных исходов испытания. Понятие равновозможности, несовместности, конечности исходов.
Аксиоматическое построение теории вероятностей. Аксиомы вероятностей. Теоремы сложения и умножения вероятностей, следствия из них. Понятие зависимых и независимых событий. , где m- число элементарных исходов испытания, благоприятствующих появлению события А; n- общее число возможных элементарных исходов испытания. Понятие равновозможности, несовместности, конечности исходов.
Аксиоматическое построение теории вероятностей. Аксиомы вероятностей. Теоремы сложения и умножения вероятностей, следствия из них. Понятие зависимых и независимых событий.
| ОК-13, ПК-1,ПК-4
|
| Тема 1.2 Правило умножения вероятностей для любого числа перемножаемых событий. Условная вероятность. Формула полной вероятности. Формула Байеса
| Правило умножения вероятностей для любого числа перемножаемых событий. Условная вероятность. Условия применимости формулы полной вероятности и формулы Байеса. Формула полной вероятности и формула Байеса.
| ОК-13, ПК-1,ПК-4
|
| Тема 1.3 Схема Бернулли. Формула Бернулли. Теорема Муавра- Лапласа
| Понятие независимых испытаний. Формула Бернулли и условия ее применимости. Необходимость использования локальной и интегральной теорем Муавра- Лапласа и формул, вытекающих из этих теорем. Локальная и интегральная теоремы Муавра- Лапласа. Оценка отклонения относительной частоты от постоянной вероятности. Наивероятнейшее число появлений события в независимых испытаниях
| ОК-13, ПК-4, ПК-6
|
|
| Раздел 2. Случайные величины
| Тема 2.1 Случайная величина. Закон распределения дискретной случайной величины
| Понятие случайной величины. Классификация случайных величин. Закон распределения случайной величины. Понятие многоугольника распределения случайной величины.
| ОК-13, ПК-1
|
| Тема 2.2 Числовые характеристики. Свойства числовых характеристик
| Понятие математического ожидания, дисперсии, среднего квадратического отклонения случайной величины, их свойства. Формулы для вычисления числовых характеристик дискретных случайных величин. Вероятностный смысл этих характеристик.
| ОК-13, ПК-4,ПК-13
|
| Тема 2.3 Непрерывные случайные величины. Плотность распределения вероятности. Свойства
| Понятие непрерывной случайной величины, функции распределения, плотности распределения вероятностей случайных величин. Построение этих функций. Свойства интегральной и дифференциальной функций распределения. Связь между интегральной и дифференциальной функциями.
| ОК-13, ПК-6
|
| Тема 2.4 Числовые характеристики непрерывной случайной величины
| Понятие математического ожидания, дисперсии, среднего квадратического отклонения, моды, медианы, начального теоретического момента порядка к, центрального теоретического момента порядка к непрерывной случайной величины, их свойства. Формулы для вычисления числовых характеристик непрерывных случайных величин. Вероятностный смысл этих характеристик.
| ОК-13, ПК-1
|
| Тема 2.5 Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Следствия из закона больших чисел. Теорема Бернулли
| Практическое и теоретическое значение неравенства Чебышева. Две формы записи неравенства Чебышева. Закон больших чисел, выраженный в форме Чебышева. Условия, при которых закон больших чисел применим к последовательности случайных величин.
| ОК-13, ПК-6
|
| Тема 2.6 Непрерывное распределение, равномерное, экспоненциальное. Параметры распределения
| Различные законы распределения случайной величины: закон равномерной плотности, показательное распределение, непрерывное распределение. Числовые характеристики случайных величин, распределенных по различным законам.
| ОК-13, ПК-1,ПК-4,ПК-13
|
|
| Тема 2.7 Нормальное распределение непрерывной случайной величины. Нормальная кривая
| Закон нормального распределения непрерывной случайной величины. Понятие нормального закона распределения как предельного закона распределения.
| ОК-13, ПК-1,ПК-4,ПК-13
|
| Тема 2.8 Вероятность попадания в заданный интервал непрерывной случайной величины. Вычисление вероятности заданного отклонения. Правило «трех сигм»
| Вычисление вероятности попадания в заданный интервал непрерывной случайной величины. Вычисление вероятности заданного отклонения. Правило «трех сигм».
| ОК-13, ПК-1,ПК-6,ПК-13
|
|
| Тема 3 Математическая статистика
| Тема 3.1 Основные задачи математической статистики. Генеральная совокупность и выборочная совокупность
| Понятие генеральной совокупности и выборочной совокупности. Вариационный ряд. Статистическое распределение выборки. Интервальный статистический ряд. Эмпирическая функция распределения и ее свойства. Полигон и гистограмма.
| ОК-13, ПК-6,ПК-4
|
| Тема 3.2 Выборочная функция распределения, выборочное среднее, выборочная дисперсия, выборочный момент
| Понятие статистической оценки параметров распределения. Генеральная средняя. Выборочная средняя. Генеральная дисперсия. Выборочная дисперсия.
| ОК-13, ПК-6, ПК-13
|
| Тема 3.3 Понятие точечной оценки, ее несмещенности и состоятельности. Метод моментов. Метод наибольшего правдоподобия.
| Понятие статистической оценки параметров распределения. Понятие точечной оценки, несмещенности, состоятельности. Метод моментов. Метод наибольшего правдоподобия для дискретных и непрерывных случайных величин.
| ОК-1, ПК-3, ПК-13
|
| Тема 3.4 Понятие доверительного интервала. Построение доверительного интервала для математического ожидания нормально распределенной случайной величины
| Понятие доверительного интервала, доверительной вероятности (надежности) оценки. Интервальная оценка математического ожидания нормально распределенного признака
| ОК-1, ПК-1, ПК-4
|
|
|
| Тема 3.5 Построение доверительного интервала для случайной величины, когда дисперсия известна
| Понятие доверительного интервала, доверительной вероятности (надежности) оценки. Оценка математического ожидания признака при известном среднем квадратическом отклонении.
| ОК-13, ПК-1,ПК-4,ПК-13
|
|
|
| Тема 3.6 Построение доверительного интервала для математического ожидания случайной величины, когда дисперсия неизвестна
| Понятие доверительного интервала, доверительной вероятности (надежности) оценки. Оценка математического ожидания признака при неизвестном среднем квадратическом отклонении.
| ОК-13, ПК-1,ПК-4,ПК-13
|
|
|
| Тема 3.7 Проверка статистических гипотез
| Понятие статистической гипотезы. Нулевая и конкурирующая гипотеза. Критическая область. Область принятия гипотезы. Основной принцип проверки статистических гипотез. Проверка гипотезы по критерию Пирсона. Проверка гипотезы о распределении генеральной совокупности по различным законам.
| ОК-13, ПК-1,ПК-4,ПК-13
|

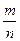 , где m- число элементарных исходов испытания, благоприятствующих появлению события А; n- общее число возможных элементарных исходов испытания. Понятие равновозможности, несовместности, конечности исходов.
Аксиоматическое построение теории вероятностей. Аксиомы вероятностей. Теоремы сложения и умножения вероятностей, следствия из них. Понятие зависимых и независимых событий.
, где m- число элементарных исходов испытания, благоприятствующих появлению события А; n- общее число возможных элементарных исходов испытания. Понятие равновозможности, несовместности, конечности исходов.
Аксиоматическое построение теории вероятностей. Аксиомы вероятностей. Теоремы сложения и умножения вероятностей, следствия из них. Понятие зависимых и независимых событий.