Модуль полного ускорения точки найдем по формуле (11.44), т. е

Или

Или

Откуда, на основании формул (11.66) и (11.67),

Ускорения точек тела, вращающегося вокруг неподвижной оси

Окончательно получим

Х, y, z — координаты точки М.

Эта формула называется формулой Эйлера.

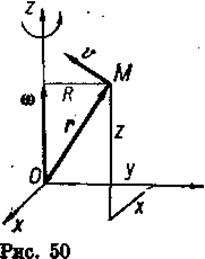
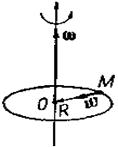
Выбрав оси координат, как указано на рис. 50, уста­новим формулы для проекций линейной скорости на оси координат, как проекций векторного произведения.

υ_x=ω_yr_z - ω_zr_y

υ_y=ω_zr_x - ω_xr_z

υ_z=ω_xr_y - ω_yr_x

где r_х = х, r_y = у, r_z = z, ω_x= 0, ω_у = 0, ω_z = ω;

υ_x = — ωy,

υ_y = ωx,

υ_z =0.

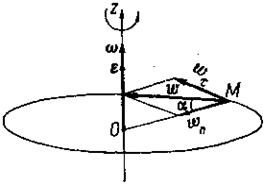
Так как в рассматриваемом случае движение точки задано естест­венным способом, то полное ускорение точки можно вычислить, как векторную сумму касательного ω_τ и нормального ω_n ускорений (см. глава I, § 16). Выразим эти ускорения через кинематические характеристики вращательного движения тела, т. е_; через ω и ε.

Имеем ω_n=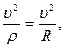 ω_τ=s,

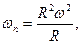
ω_n = R ω²

и

ω_τ = s== Rφ,

ω_τ = Rε.

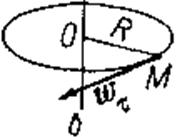
Следовательно, нормальное ускорение точки тела при вращении его вокруг неподвижной оси равно произведению радиуса вращения на квадрат угловой скорости. Касательное ускорение равно произведе­нию радиуса вращения на угловое ускорение. Нормальное ускорение направлено по радиусу вращения к центру вращения (рис. 51, а). Касательное ускорение направлено по касательной к траектории в сторону вращения, если движение ускоренное (ε > 0), и в сторо­ну, противоположную вращению, если движение замедленное, т. е. ε< 0 (рис. 51, б, в).

Дата добавления: 2013-12-12