Теорема. При плоско-параллельном движении твердого тела скорость любой его точки равна векторной сумме скорости полюса и скорости во вращательном движении вокруг полюса

Скорости точек тела

Кинематические уравнения плоско-параллельного движения

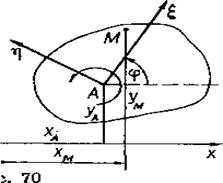
Допустим, что плоская фигура движется в неподвиж­ной плоскости Оху. Выбрав, например, точку А плоской фигуры за полюс, неизменно свяжем с этой фигурой подвижную систему координат Аξη с началом в полюсе А (рис. 70). Для определения положения подвижной системы координат Аξη относительно не­подвижной нужно знать координаты точки А (т. е. х_A и у_A), а также угол поворота φ вокруг полюса (т. е. угол, образованный осью Аξη с осью Ох). Следователь­но, кинематические уравнения плоско-параллельного движения твердого тела имеют вид

x_A= x_A(t). y_A = y_A (t). φ = φ (t),

где x_A(t) y_A (t), φ (t) — конечные, однозначные, непрерывные и дифференцируемые функции времени.

Пользуясь формулами преобразования координат, можно полу­чить уравнения движения любой точки М плоской фигуры

x = x_A + ξcos φ —ηsin φ,

y = y_A + ξsin φ + ηcos φ -

Доказательство. Пусть полюс О движется со скоростью υ₀, а плоская фигура вращается вокруг полюса с угловой скоростью ω (рис. 71). Требуется определить скорость произвольной точки М этой фигуры. Так как переносным здесь является поступательное движение вместе с полюсом О, то переносные скорости всех точек плоской фигуры будут одинаковыми, равными скорости полюса:

υ _Me= υ ₀

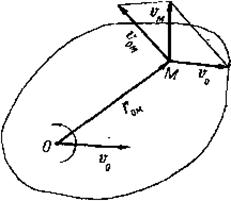
Относительным движением является вращательное движение вокруг полюса. Поэтому, обозначая радиус-вектор точки М относитель­но полюса О через r _OM, согласно формуле Эйлера, для относительной скорости точки М получим

υ _Mr= ω x r _OM.

Относительную скорость точки при плоско-парал­лельном движении тела обозначают двойным индексом, т. е. υ _Mr = υ _OM. Первый индекс указывает полюс О, вокруг которого происходит вращение, а второй — обозначает рассматриваемую точку М. Следовательно,

υ _Mr= υ _OM= ω x r _OM

По теореме о сложении скоростей получим

υ _a= υ _e+ υ _r.

Следовательно,

υ _M= υ _O+ υ _OM.

Дата добавления: 2013-12-12