Множества в пространстве . Непрерывные отображения

Глава 4. Дифференциальное исчисление функций нескольких переменных.

Схема полного исследования функции. Построение графика.

1. Область определения функции.
2. Симметрия графика, периодичность.
3. Точки разрыва функции и их классификация.
4. Точки пересечения графика с осями координат, интервалы знакопостоянства.
5. Асимптоты графика и подходы к ним.
6. Интервалы монотонности и точки экстремума функции.
7. Интервалы выпуклости и точки перегиба функции.
8. Нахождение дополнительных точек графика.
9. Построение графика функции.

Пример. Провести исследование функции 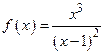и построить ее график

1. Область определения функции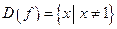

2. Функция непериодическая, ни чётная, ни нечетная (функция общего вида).

3. 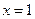− точка бесконечного разрыва функции.

4. 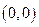− единственная точка пересечения с осями координат. , .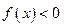

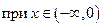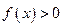
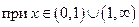5. Вертикальная асимптота: 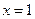. Подходы к асимптоте: 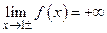. Наклонная асимптота: 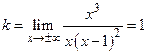. 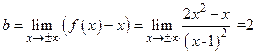, 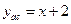. Подходы к асимптоте: 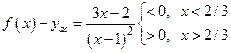. Пересечения с асимптотой − .

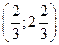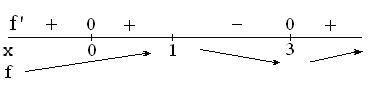
6. 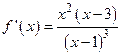Точка минимума .
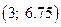7. 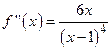Точка перегиба ─ .

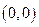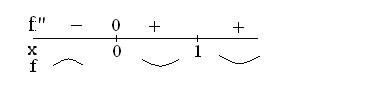
8. Дополнительные точки графика: .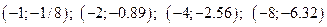

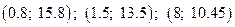
9. Построение графика функции.

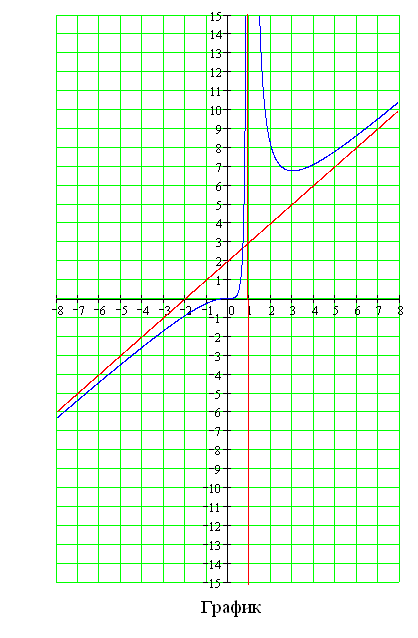
1⁰. Мы имели дело раньше в основном с функциями вида , 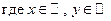. Встречались мы и с кривыми, задаваемыми параметрическими уравнениями 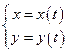. Здесь мы имеем 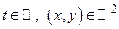. Это − отображение типа 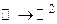. В случае пространственной кривой получаем отображение типа 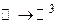. В геометрии приходится рассматривать поверхности с уравнением вида 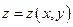, то есть отображения типа .

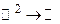Нам предстоит изучать отображения типа 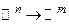. Поэтому придется сначала познакомиться с множествами 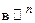(вместо 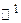обычно пишут просто ).

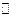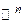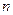− -мерное координатное пространство. Оно состоит из наборов действительных чисел 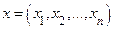. Мы будем рассматривать их и как векторы и как точки. Нулевым вектором называется вектор 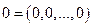. Векторы можно покоординатно складывать и покоординатно умножать на скаляр. Длина вектора 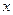вычисляется по формуле 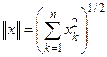. Напомним основные свойства функции .

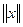1. 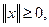при этом 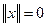тогда и только тогда, когда .

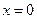2. 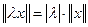для любого скаляра .

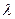3. 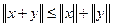(неравенство треугольника).

Обобщением длины является норма. Это − любая числовая функция в 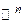, обладающая свойствами 1-2-3. Они называются аксиомами нормы. В качестве примера рассмотрим функцию 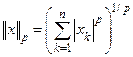. Можно доказать, что 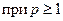эта функция удовлетворяет аксиомам нормы.

Длина или евклидова норма − это , , .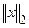

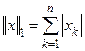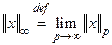Упражнение 1. Доказать, что .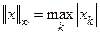

Упражнение 2. Доказать неравенства: , , .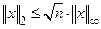

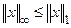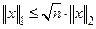Расстоянием между точкам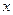и и называют величину 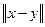. Открытым шаром в пространстве 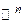называется множество 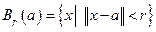; точка 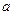называется 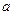центром шара, число 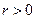− его радиусом.

Упражнение 3. Нарисовать единичный шар (круг) на плоскости 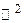для норм 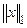, 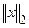и .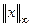

В дальнейшем 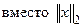будем писать просто .

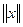Множество 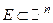называется ограниченным, если его можно покрыть некоторым шаром.

Последовательность точек 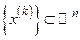называется сходящейся (по норме), если существует точка 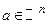, для которой 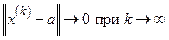(в записи 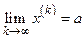). Последовательность 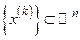покоординатно сходится к точке 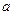, если при каждом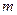 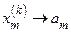. Неравенства из упражнения 2 показывают, что покоординатная сходимость в пространстве 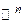равносильна сходимости по норме.

Точка 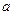называется внутренней точкой множества 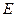, если существует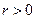такое, что 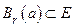. Множество 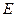называется открытым, если все его точки являются внутренними.

Точка 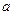называется предельной точкой множества 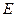, если 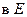существует последовательность 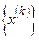, которая сходится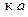. Множество 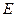называется замкнутым, если оно содержит все свои предельные точки.

Примеры. На числовой прямой 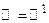интервал 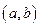− открытое множество, отрезок 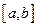− замкнутое множество, а полуинтервал 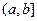ни замкнут, ни открыт. В пространстве 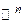шар 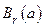− открытое множество.

Множество 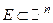называется связным, если любые две точки этого множества можно соединить ломанной, лежащей внутри этого множества.

В пространстве 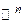, как и в пространстве 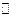, справедлива теорема Больцано-Вейерштрасса и критерий Коши.

Теорема Больцано-Вейерштрасса. Из ограниченной бесконечной последовательности можно выделить сходящуюся подпоследовательность.

Дата добавления: 2013-12-13