
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства градиента. Касательная плоскость и нормаль к поверхности
|
|
|
|
Пример 1.Пусть.Тогда.
Определение 3. Градиентом функции  в точке
в точке 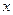 называется вектор
называется вектор  , имеющий в стандартном базисе координаты
, имеющий в стандартном базисе координаты 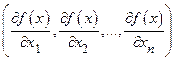 . Более краткое обозначение градиента
. Более краткое обозначение градиента  (значок
(значок 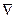 читается “ набла ”).
читается “ набла ”).
Определение 4. Пусть  . Матрицей Якóби этого отображения в точке
. Матрицей Якóби этого отображения в точке 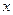 называется матрица
называется матрица 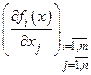 , состоящая из производных от каждой компоненты по каждой координате. Производная
, состоящая из производных от каждой компоненты по каждой координате. Производная 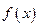 по вектору
по вектору 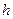 определяется так же, как и раньше.
определяется так же, как и раньше.
Определение 5. Отображение 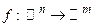 называется дифференцируемым в точке
называется дифференцируемым в точке 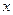 , если его полное приращение
, если его полное приращение 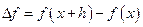 может быть представлено в виде
может быть представлено в виде
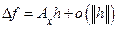
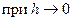 , где
, где 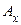 − линейный оператор, то есть отображение, обладающее свойством линейности:
− линейный оператор, то есть отображение, обладающее свойством линейности: 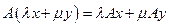 . Оператор
. Оператор 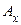 действует из пространства
действует из пространства 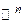 в пространство
в пространство  . Он называется производным отображением и обозначается
. Он называется производным отображением и обозначается 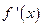 . Выражение
. Выражение  или
или 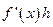 называется дифференциалом
называется дифференциалом  и обозначается
и обозначается 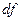 . Очевидно, что из дифференцируемости следует непрерывность.
. Очевидно, что из дифференцируемости следует непрерывность.
Теорема 1. (Необходимое условие дифференцируемости). Если отображение  дифференцируемо в точке
дифференцируемо в точке 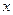 , то в этой точке существуют все частные производные и даже производные по любому вектору
, то в этой точке существуют все частные производные и даже производные по любому вектору  . При этом
. При этом  . Однако, в отличие от случая функций одной переменной, из существования производной по любому вектору не следует дифференцируемость отображения.
. Однако, в отличие от случая функций одной переменной, из существования производной по любому вектору не следует дифференцируемость отображения.
Доказательство. Пусть 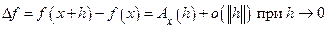 . Тогда
. Тогда 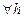
 .
.
Поэтому 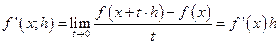 . Отсутствие обратной импликации видно, например, из следующего контрпримера.
. Отсутствие обратной импликации видно, например, из следующего контрпримера.
Контрпример. Пусть  . У этой функции существует производная в точке
. У этой функции существует производная в точке 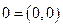 по любому вектору
по любому вектору 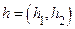 и эта производная равна
и эта производная равна  . Если бы функция была дифференцируемой в точке
. Если бы функция была дифференцируемой в точке 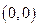 , выражение
, выражение  линейно зависело бы от вектора
линейно зависело бы от вектора 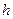 . То есть было бы
. То есть было бы 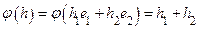 . Однако, не всегда
. Однако, не всегда 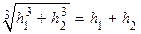 . Так, например,
. Так, например, 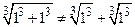 или
или 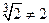 .
.
Следствие. Если отображение  дифференцируемо в точке
дифференцируемо в точке 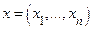 , то в этой точке существуют все частные производные
, то в этой точке существуют все частные производные  , а матрицей линейного
, а матрицей линейного
оператора 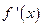 в стандартном базисе является матрица Якоби.
в стандартном базисе является матрица Якоби.
Доказательство*. Обозначим 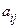 матричные элементы
матричные элементы  в базисе
в базисе 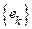 . Тогда будет
. Тогда будет 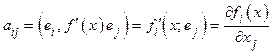 .
.
Теорема 2. (Достаточное условие дифференцируемости). Если все частные производные  существуют в окрестности точки
существуют в окрестности точки 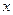 и непрерывны в самой точке, то отображение
и непрерывны в самой точке, то отображение  дифференцируемо в этой точке.
дифференцируемо в этой точке.
Доказательство. Достаточно при указанных условиях доказать дифференцируемость скалярной функции, то есть одной компоненты отображения  . Метод доказательства проще понять в случае
. Метод доказательства проще понять в случае  . Мы имеем
. Мы имеем
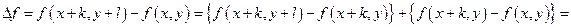
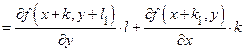 , где число
, где число  заключено между числами
заключено между числами 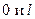 , а
, а 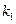 заключено между числами
заключено между числами 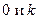 (теорема Лагранжа).
(теорема Лагранжа).
Если 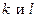 стремятся к нулю, то стремятся к нулю, то 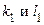 также стремятся к нулю. Воспользовавшись непрерывностью производных также стремятся к нулю. Воспользовавшись непрерывностью производных  и и  в точке в точке 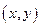 , получим , получим 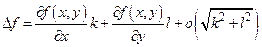  . Ч и т.д. . Ч и т.д.
| 
|
1о. Рассмотрим скалярное поле, то есть функцию 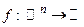 . Если функция f дифференцируема в точке
. Если функция f дифференцируема в точке 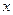 , то, как мы уже знаем,
, то, как мы уже знаем,  . В нашем случае это означает, что
. В нашем случае это означает, что
 или
или  .
.
Так как направляющие косинусы вектора 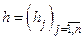 равны
равны 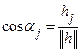 , то вектор
, то вектор 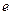 единичной длины равен
единичной длины равен 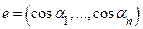 . Мы получаем формулу для вычисления производной по направлению:
. Мы получаем формулу для вычисления производной по направлению:
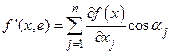 .
.
Неравенство Коши показывает, что 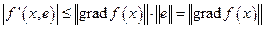 . Равенство здесь возможно лишь, если векторы
. Равенство здесь возможно лишь, если векторы 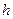 и
и  коллинеарны. Таким образом, производная по направлению
коллинеарны. Таким образом, производная по направлению 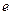 принимает наибольшее значение, если
принимает наибольшее значение, если 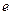 коллинеарен вектору
коллинеарен вектору  . Равно это наибольшее значение
. Равно это наибольшее значение 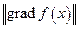 . Отсюда следует, что градиенту можно дать новое (бескоординатное) определение.
. Отсюда следует, что градиенту можно дать новое (бескоординатное) определение.
Определение. Градиент функции  в точке
в точке 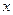 − это вектор, длина которого равна наибольшей из производных
− это вектор, длина которого равна наибольшей из производных  по всевозможным направлениям в точке
по всевозможным направлениям в точке 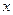 . Направление градиента совпадает с направлением наиболее быстрого возрастания функции
. Направление градиента совпадает с направлением наиболее быстрого возрастания функции  в этой точке.
в этой точке.
Мы видим, что градиент скалярного поля (функции) не зависит от выбора координат, а определяется самим полем.
Отметим, что по направлению “минус градиента” функция быстрее всего убывает, а по направлениям, перпендикулярным к градиенту, функция  имеет нулевую скорость изменения, так как, если
имеет нулевую скорость изменения, так как, если 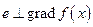 , то
, то 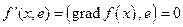 .
.
2о. Рассмотрим поверхность 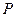 , заданную неявным уравнением
, заданную неявным уравнением  , где
, где 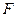 дифференцируема в точке
дифференцируема в точке  , лежащей на этой поверхности, причем градиент
, лежащей на этой поверхности, причем градиент 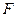 отличен от нуля в этой точке (такая точка
отличен от нуля в этой точке (такая точка 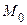 называется регулярной). Все прямые, проходящие через эту точку и перпендикулярные вектору
называется регулярной). Все прямые, проходящие через эту точку и перпендикулярные вектору  , лежат в одной плоскости, которая называется касательной плоскостью к поверхности
, лежат в одной плоскости, которая называется касательной плоскостью к поверхности  в точке
в точке 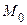 . Уравнение касательной плоскости
. Уравнение касательной плоскости  имеет вид
имеет вид
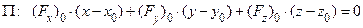 .
.
Приведём ещё канонические уравнения нормали (т.е. прямой 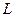 , которая перпендикулярна плоскости
, которая перпендикулярна плоскости  и также проходит через точку
и также проходит через точку 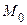 ):
):
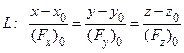 .
.
Пусть уравнение поверхности 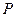 приведено к явному виду
приведено к явному виду  , где функция
, где функция  дифференцируема в точке
дифференцируема в точке 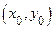 . Если принять
. Если принять 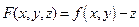 , то мы снова вернёмся к уравнению
, то мы снова вернёмся к уравнению 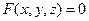 . Сейчас
. Сейчас 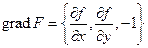 , поэтому уравнение касательной плоскости
, поэтому уравнение касательной плоскости  примет вид
примет вид
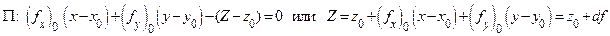 ,
,
где 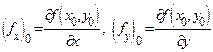 (сравните с уравнением касательной к графику
(сравните с уравнением касательной к графику  ).
).
Ясно, что  , когда
, когда  . Таким образом, касательная плоскость
. Таким образом, касательная плоскость  в окрестности точки
в окрестности точки 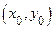 прилегает к поверхности
прилегает к поверхности 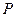 теснее, чем любая другая плоскость.
теснее, чем любая другая плоскость.
Уравнения нормали сейчас приобретают вид
 .
.

|
Пример. Составить уравнения касательной плоскости и нормали к эллипсоиду 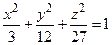 в точке
в точке 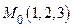 .
.
Решение. Прежде всего, т. 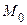 принадлежит данной поверхности, т.к.
принадлежит данной поверхности, т.к. 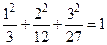 .
.
1-й способ. Т.к.  , то
, то 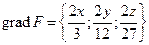 ,
, 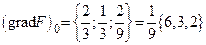 . Можно считать, что нормальный вектор касательной плоскости равен
. Можно считать, что нормальный вектор касательной плоскости равен 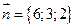 .
.
Поэтому получаем уравнения 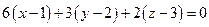 и
и  .
.
2-й способ: 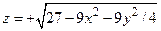 . Следовательно,
. Следовательно, 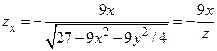 ,
, 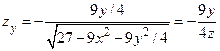 ,
, 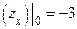
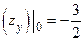 . Поэтому уравнение касательной плоскости имеет вид:
. Поэтому уравнение касательной плоскости имеет вид: 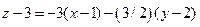 или
или 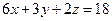 , а канонические уравнения нормали:
, а канонические уравнения нормали:  .
.
Упражнение. Доказать, что уравнение касательной плоскости к эллипсоиду с уравнением  в точке
в точке 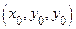 , лежащей на этой поверхности, имеет вид
, лежащей на этой поверхности, имеет вид  .
.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 6182; Нарушение авторских прав?; Мы поможем в написании вашей работы!