Под множеством будем понимать любую совокупность определенных и различимых между собой объектов, рассматриваемую как единое целое

Основные понятия

Введение

Содержание

Основы теории множеств

П.С. Довгий, В.И. Поляков

Кафедра вычислительной техники

Cанкт-Петер­бургс­кий государ­ст­вен­ный университет

Высшего профессионального образования

Государственное образовательное учреждение

Министерство образования и науки Российской Федерации

информационных тех­но­логий, механики и оп­тики”

Конспект лекций по дисциплине

«Дискретная математика»

Санкт-Петербург

2011 г.

Введение
Основные понятия
Способы задания множеств
Отношения между множествами
Алгебра множеств
Операции над множествами
Основные тождества (законы) алгебры множеств
Способы доказательства тождеств
Упорядоченные множества
Понятие вектора
Прямое (декартово) произведение множеств
Декартова степень множества
Мощность прямого произведения множеств
Основные тождества для операции прямого произведения множеств
Литература
Контрольные вопросы
Контрольные задачи

Вряд ли можно назвать какую-либо возникшую в последней трети девятнадцатого века математическую дисциплину, которая оказала бы большее влияние на прогресс всей математики и, шире, на математическое мышление в целом, чем теория множеств. К идеям теории множеств в разное время подходили с разных сторон многие ученые, но оформление ее в самостоятельную науку, со своими особыми предметом и методом исследования, осуществил в своих работах 1872-1897 г.г. немецкий математик Георг Кантор. Среди современников Г. Кантора правильно оценили значение этих работ только немногие, прежде всего Рихард Дедекинд, который внес собственный значительный вклад в новую теорию. Обнаруженные в конце ХIХ — начале ХХ вв. логические и методологические парадоксы теории множеств отпугнули некоторых выдающихся математиков, первоначально приветствовавших ее появление, в частности, таких как Анри Пуанкаре. Однако плодотворные приложения теории множеств в различных разделах математики стимулировали ее дальнейшую разработку во многих направлениях и исследование самых ее основ средствами бурно развивавшейся математической логики. Какие-либо окончательные и общепризнанные решения всех сложных проблем до сих пор не достигнуты и все более и более тонкие изыскания здесь продолжаются; вместе с тем современная математика не может обойтись без основного аппарата, понятий и приемов теории множеств.

Г. Кантору принадлежит заслуга привнесения в математику самого понятия "множества" (или "совокупности"). Это понятие относится к категории фундаментальных и неопределяемых понятий математики. Его можно толковать и иллюстрировать лишь на примерах. " Под множеством - писал Г. Кантор - я понимаю вообще всякое многое, мыслимое нами как единое, т.е. всякую совокупность определенных элементов, которая может быть связана в одно целое с помощью некоторого закона..." (Кантор Г. Труды по теории множеств. - М.: Наука, 1985. - С. 101) Г. Кантору принадлежит также следующая формулировка понятия множества: «Множество — это объединение определённых, различных объектов, называемых элементами множества, в единое целое».

Георг Кантор (1845 -1918)

В основе теории множеств лежат первичные понятия: множество и отношение «быть элементоммножества».

Объекты, образующие некоторое множество, называются его элементами. Принадлежность некоторого элемента x множеству A обозначается как x Î A — «x есть элемент множества A» или «x принадлежит множеству A». В свою очередь непринадлежность некоторого элемента а множеству М обозначается в виде: а Ï М или а 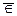М. Множества принято обозначать заглавными буквами латинского алфавита, а элементы множеств – строчными буквами.

Среди производных понятий теории множеств наиболее важны следующие.

· Пустое множество. Пустым множеством называется множество, не содержащее ни одного элемента. Пустое множество обозначают символом Æ.

· Подмножество и надмножество. Множество A называется подмножеством множества B, если любой элемент, принадлежащий A, также принадлежит B. Это записывается в виде отношения включения: A Í B. Таким образом, (A Í B) Û (x Î A ® x Î B). Множество B, в свою очередь, называется надмножеством множества A, что записывается в виде отношения обратного включения: B Ê A.

Пустое множество является подмножеством любого множества.

· Универсальное множество. Обычно, в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества, своего для каждого случая, которое называется универсальным множеством (универсумом). Универсальное множество обычно обозначается U (от англ. universe, universal set), реже E.

· Мощность множества можно рассматривать как числовую характеристику (метрику) любого множества. Мощностью некоторого конечного множества А является число его элементов. Мощность множества А принято обозначать | А |, например, мощность множества А= { a, b, c } равна | А |=3.

Мощность пустого множества равна нулю: | Æ |=0.

· Конечные и бесконечные множества. Множества, имеющие конечное число элементов и, соответственно, конечное значение мощности называются конечными, а множества с бесконечным числом элементов и, соответственно, с бесконечной мощностью - бесконечными.

Множества, обладающие одинаковым значением мощности, называются равномощными. Понятие равномощности распространяется и на бесконечные множества.

· Счетные и несчетные множества. Бесконечные множестваразделяются на счётные и несчетные. Бесконечное множество называется счетным, если его элементы можно пронумеровать, в противном случае, бесконечное множество называется несчетным.

Простейшим примером счетного множества является множество всех натуральных чисел, в связи с чем можно дать другое определение счетного множества: множество называется счетным, если оно равномощно множеству натуральных чисел, т.е. его можно представить в виде { x₀, x₁, x₂, … }, где х_i – элемент множества, однозначно соответствующий его номеру (индексу) i.

В свою очередь, простейшим примером несчетного множества является множество действительных чисел.

Другими примерами счетных множеств являются множества целых и рациональных чисел, а примером несчетного множества – множество комплексных чисел.

В отношении счетных множеств имеют место следующие теоремы:

- любое подмножество счетного множества является либо конечным, либо счетным, иначе говоря, каждое бесконечное подмножество счетного множества также является счетным;

- объединение конечного числа счетных множеств также является счетным множеством.

· Булеан множества. Любое конечное множество содержит и конечное число подмножеств. Связь между произвольным множеством и всеми его подмножествами определяется булеаном.

Булеа­ном множества А называется множество всех его подмножеств. Булеа­н множества А будем обозначать В (А).

Иначе булеан множества А называют множеством - степенью множества А.

Булеан как множество всех подмножеств множества А должен включать в себя:

- пустое множество;

- само множество А;

- отдельные элементы множества А;

- всевозможные комбинации различных элементов множества А.

Замечание. Если множество А содержит n элементов, то число его подмножеств из k элементов представляет собой число сочетаний из n по k и определяется по формуле:

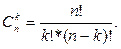
Пример 1. Записать булеан (множество – степень) для множества А= { a, b, c }.

Дата добавления: 2013-12-13