Способы доказательства тождеств

Законы поглощения: АÈ (АÇВ)=А; АÇ(АÈВ)=А.

7). Закон инволютивности: .

8) Закон противоречия: А Ç=Æ.

9) Закон «третьего не дано» (исключенного третьего): А È= U.

10) Свойства универсального множества: А È U = U; А Ç U = А.

11) Свойства пустого множества: А ÈÆ= А; А ÇÆ=Æ.

Дополнительные тождества для операций объединения, пересечения и дополнения множеств:

12) Законы склеивания:

13) Законы сокращения (законы Порецкого):

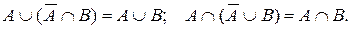
Следствия из законов сокращения:

14) Дополнительные тождества (законы) для операции разности (относительного дополнения) множеств: A\ (B\C)=(A\B) È (A Ç C); (A\B)\ C= (A\C)\(B\C);

A\ (B È C)=(A\B)\ C; A\ (B È C)=(A\C)\(B\C).

15) Дополнительные тождества (законы) для операции симметрической разности:

A Δ(B Δ C)=(A Δ B) Δ C; A Ç(B Δ C)=(A Ç B) Δ(A Ç C).

Замечание. Практически все основные тождества (законы) множеств представлены парами, которые характеризуются своей симметричностью в отношении операций объединения и пересечения. Подобное свойство законов называется дуальностью (двойственностью). С учетом этого свойства можно выразить один закон пары из другого путем замены операции объединения на операцию пересечения и наоборот. Это относится к законам 1-6. Что касается законов 8-11, то их также можно представить парами, но в отличии от законов 1-6 один закон пары получается из другого не только заменой операций, но и стандартных множеств (универсума и пустого) на противоположное.

Кроме того, свойством дуальности обладают также законы 12 и 13.

Огастес де Морган, (1806-1871) шотландский математик и логик.

Порецкий Платон Сергеевич (1846 -1907) русский математик, астроном и логик.

Убедиться в справедливости тождеств можно с помощью диаграмм Эйлера-Венна. Для этого необходимо изобразить на диаграммах левую и правую части тождеств и сравнить их. Такой способ доказательства принято называть геометрическим. Этот способ является наглядным, но не обладает достаточной строгостью.

Пример 6. Проверим первый дистрибутивный закон: А È(В Ç С)=(А È В)Ç(А È С) (рис.4).

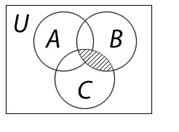
Диаграммы левой и правой частей тождества совпадают,

значит оно справедливо.

В Ç С А È(В Ç С)

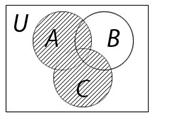
А È В А È С (А È В)Ç(А È С)

Рис. 4. Проверка дистрибутивного закона на диаграммах Эйлера-Венна

Пример 7. Проверим справедливость правила де Моргана на диаграммах Эйлера-Венна (рис. 5).

Диаграммы левой и правой

частей тождества совпадают,

значит оно справедливо.

А È В

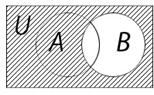
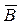
Ç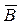

Рис. 5. Проверка правила де Моргана на диаграммах Эйлера-Венна

Доказательство справедливости проверяемых тождеств можно проводить одним из двух методов:

- методом взаимного включения;

- алгебраическим методом.

Метод взаимного включения базируется на определении равенства двух множеств, между которыми существует отношение взаимного включения: А = В Û А Í ВиВ Í А.

Пример 8. Докажем первый дистрибутивный закон: А È(В Ç С)=(А È В)Ç(А È С).

Обозначим левую часть тождества А È(В Ç С) через D_l, а правую – (А È В)Ç(А È С) через D_r.

В соответствии с принятым методом доказательство разделяется на две части:

1) берется произвольный элемент множества D_l (х ÎD_l) и доказывается, что он принадлежит также и множеству D_r, откуда следует: D_lÍD_r;

2) берется произвольный элемент множества D_r и доказывается, что он принадлежит также и множеству D_l, откуда следует: D_rÍ D_l.

1. Пусть элемент х Î D_l, т.е. х Î А È(В Ç С), тогда по определению операции объединения (х Î А) или (х Î В Ç С).

а) Если элемент х Î А, то, по определению операции объединения множеств,

(х Î А È В) и (х Î А È С), следовательно х Î (А È В)Ç(А È С), т.е. х ÎD_r;

б) Если элемент х Î В Ç С, то, по определению операции пересечения множеств,

(х Î В) и (х Î С), отсюда, по определению операции объединения,

(х Î А È В) и (х Î А È С), следовательно х Î(АÈВ)Ç(АÈС), т.е. х ÎD_r;.

Так как для любого х ÎD_l следует, что х ÎD_r, то, по определению отношения включения D_lÍD_r.

1. Пусть элемент х ÎD_r, т.е. (х Î А È В) и (х Î А È С), откуда по определению операции объединения (х Î Аилих Î В) и (х Î Аилих Î С), следовательно, х Î Аили (х Î Вих Î С), откуда, х Î Аили (х Î B Ç С), т.е. х Î А È(В Ç С) или х ÎD_l, откуда D_rÍD_l.

Таким образом, между множествами D_l и D_r существуют отношение взаимного включения, значит D_l=D_r, что и требовалось доказать.

Пример 9. Докажем первый закон двойственности: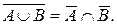

Обозначим D_l=и D_r=Ç_.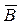

1. Пусть элемент x Î D_l, т.е. x Î . Тогда x Î Uи (x 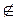А È В), значит x 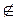Аих 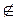В (тонкий момент в доказательстве: х не принадлежит ни А, ни В), следовательно х Î их Î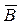, т.е. х ÎÇ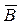. Значит D_l Í D_r.

2. Пусть теперь элемент х Î D_r, т.е. х Î Ç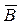. Тогда (х Î₎ и (х Î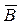₎, значит x Î Uиx одновременно не принадлежит ни А, ни В, т.е. х 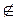(А илиВ), следовательно

х 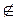А È В, т.е. х Î . Из этого следует, что D_r Í D_l.

Таким образом, между множествами D_l и D_r существуют отношение взаимного включения, значит D_l=D_r, что и требовалось доказать.

Алгебраический метод доказательства проверяемых тождеств базируется на преобразовании алгебраического выражения из левой части тождества к виду, представляющему правую часть. Как вариант модификации метода можно осуществить преобразование алгебраических выражений из обеих частей тождества путем приведения их к одному и тому же виду.

Пример 10. Докажем второй закон поглощения: А Ç(А È В) = А путем преобразования левой части тождества к правой с использованием других тождеств:

А Ç (А È В ) = (А È Æ)Ç(А È В) = (А È(Æ Ç B)) = А È Æ = А.

Ý Ý Ý Ý

свойство пустого по дистрибутивному свойства пустого

множества закону множества

Дата добавления: 2013-12-13